Subject: Reverse-engineering an analog Bendix air data computer: part 4, the Mach section
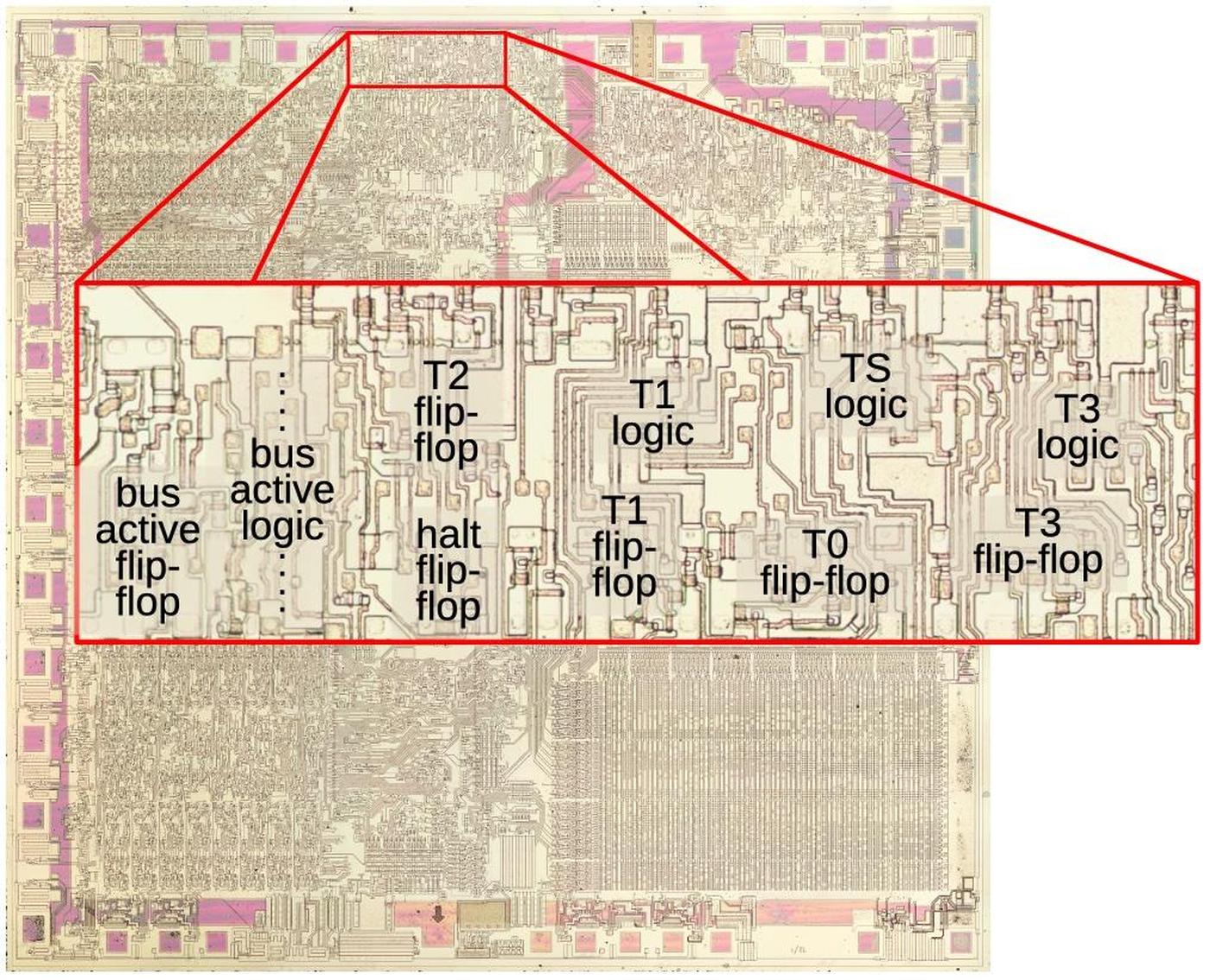
In the 1950s, many fighter planes used the Bendix Central Air Data Computer (CADC) to compute airspeed, Mach number, and other "air data". The CADC is an analog computer, using tiny gears and specially-machined cams for its mathematics. In this article, part 4 of my series,1 I reverse engineer the Mach section of the CADC and explain its calculations. (In the photo below, the Mach section is the middle section of the CADC.)
Aircraft have determined airspeed from air pressure for over a century. A port in the side of the plane provides the static air pressure,2 the air pressure outside the aircraft. A pitot tube points forward and receives the "total" air pressure, a higher pressure due to the air forced into the tube by the speed of the airplane. The airspeed can be determined from the ratio of these two pressures, while the altitude can be determined from the static pressure.
But as you approach the speed of sound, the fluid dynamics of air change and the calculations become very complicated. With the development of supersonic fighter planes in the 1950s, simple mechanical instruments were no longer sufficient. Instead, an analog computer calculated the "air data" (airspeed, air density, Mach number, and so forth) from the pressure measurements. This computer then transmitted the air data electrically to the systems that needed it: instruments, weapons targeting, engine control, and so forth. Since the computer was centralized, the system was called a Central Air Data Computer or CADC, manufactured by Bendix and other companies.
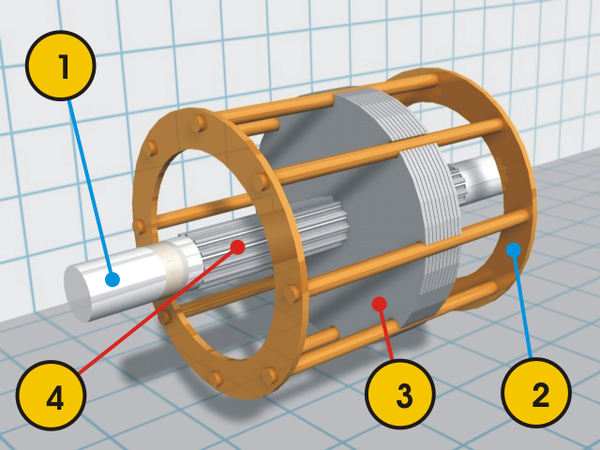
Each value in the Bendix CADC is indicated by the rotational position of a shaft. Compact electric motors rotate the shafts, controlled by the pressure inputs. Gears, cams, and differentials perform computations, with the results indicated by more rotations. Devices called synchros converted the rotations to electrical outputs that are connected to other aircraft systems. The CADC is said to contain 46 synchros, 511 gears, 820 ball bearings, and a total of 2,781 major parts (but I haven't counted). These components are crammed into a compact cylinder: just 15 inches long and weighing 28.7 pounds.
The equations computed by the CADC are impressively complicated. For instance, one equation is:
\[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]
It seems incredible that these functions could be computed mechanically, but three techniques make this possible. The fundamental mechanism is the differential gear, which adds or subtracts values. Second, logarithms are used extensively, so multiplications and divisions are implemented by additions and subtractions performed by a differential, while square roots are calculated by gearing down by a factor of 2. Finally, specially-shaped cams implement functions: logarithm, exponential, and application-specific functions. By combining these mechanisms, complicated functions can be computed mechanically, as I will explain below.
The differential
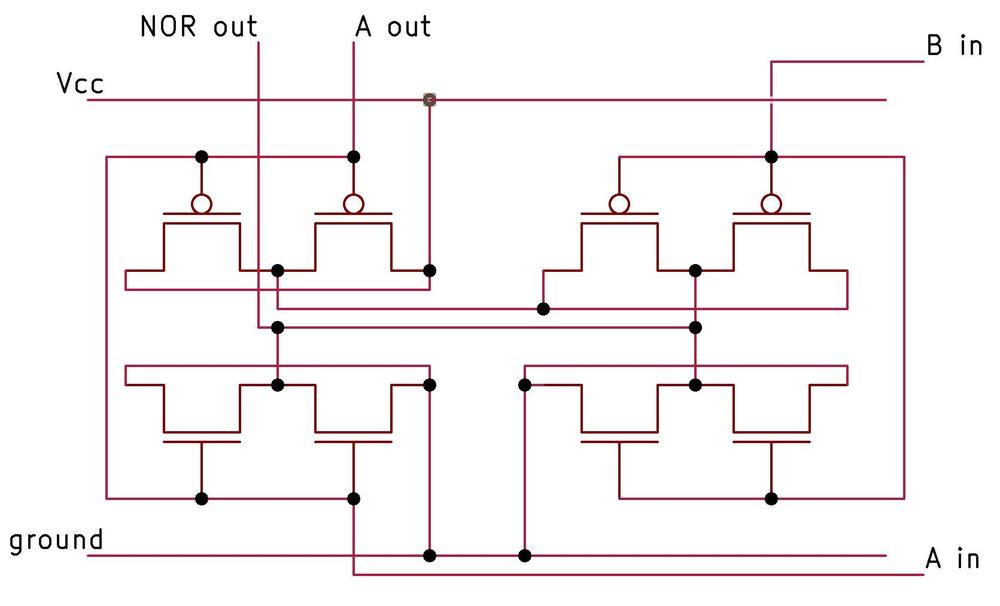
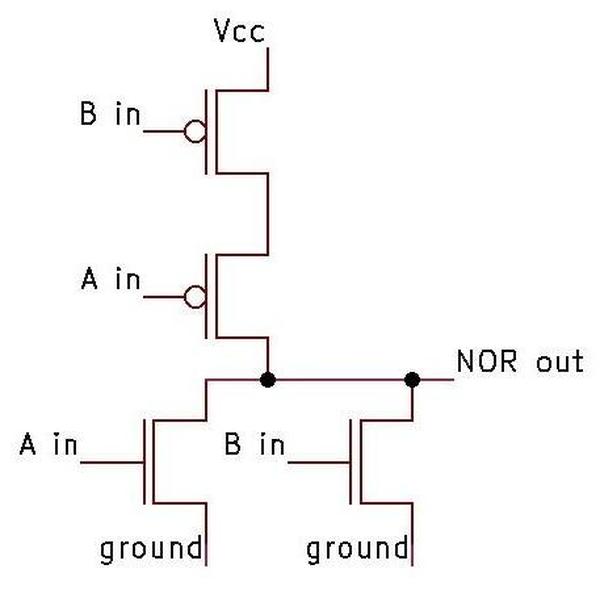
The differential gear assembly is the mathematical component of the CADC, as it performs addition or subtraction.3 The differential takes two input rotations and produces an output rotation that is the sum or difference of these rotations.4 Since most values in the CADC are expressed logarithmically, the differential computes multiplication and division when it adds or subtracts its inputs.
While the differential functions like the differential in a car, it is constructed differently, with a spur-gear design. This compact arrangement of gears is about 1 cm thick and 3 cm in diameter. The differential is mounted on a shaft along with three co-axial gears: two gears provide the inputs to the differential and the third provides the output. In the photo, the gears above and below the differential are the input gears. The entire differential body rotates with the sum, connected to the output gear at the top through a concentric shaft. (In practice, any of the three gears can be used as the output.) The two thick gears inside the differential body are part of the mechanism.
The cams
The CADC uses cams to implement various functions. Most importantly, cams compute logarithms and exponentials. Cams also implement complicated functions of one variable such as ${M}/{\sqrt{1 + .2 M^2}}$. The function is encoded into the cam's shape during manufacturing, so a hard-to-compute nonlinear function isn't a problem for the CADC. The photo below shows a cam with the follower arm in front. As the cam rotates, the follower moves in and out according to the cam's radius.
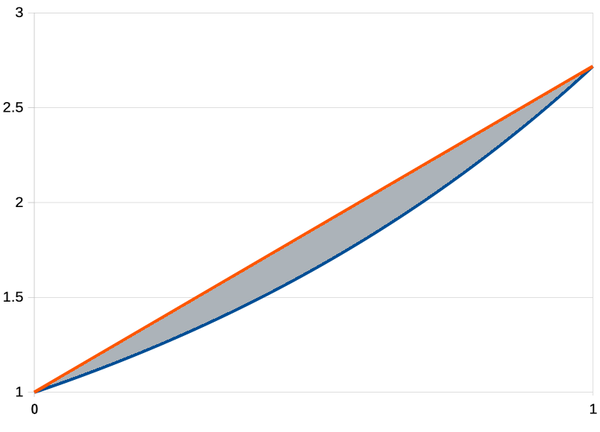
However, the shape of the cam doesn't provide the function directly, as you might expect. The main problem with the straightforward approach is the discontinuity when the cam wraps around. For example, if the cam implemented an exponential directly, its radius would spiral exponentially and there would be a jump back to the starting value when it wraps around. Instead, the CADC uses a clever patented method: the cam encodes the difference between the desired function and a straight line. For example, an exponential curve is shown below (blue), with a line (red) between the endpoints. The height of the gray segment, the difference, specifies the radius of the cam (added to the cam's fixed minimum radius). The point is that this difference goes to 0 at the extremes, so the cam will no longer have a discontinuity when it wraps around. Moreover, this technique significantly reduces the size of the value (i.e. the height of the gray region is smaller than the height of the blue line), increasing the cam's accuracy.5
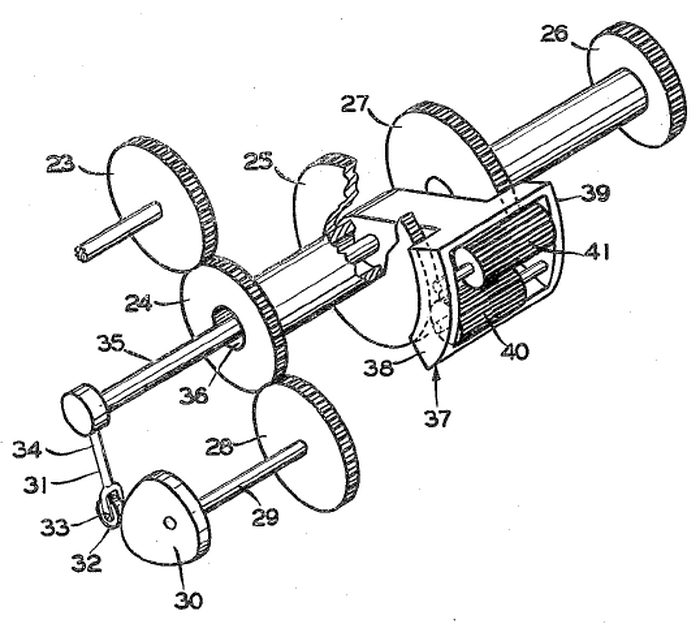
To make this work, the cam position must be added to the linear value to yield the result. This is implemented by combining each cam with a differential gear; watch for the paired cams and differentials below. As the diagram below shows, the input (23) drives the cam (30) and the differential (25, 37-41). The follower (32) tracks the cam and provides a second input (35) to the differential. The sum from the differential produces the desired function (26).
The synchro outputs
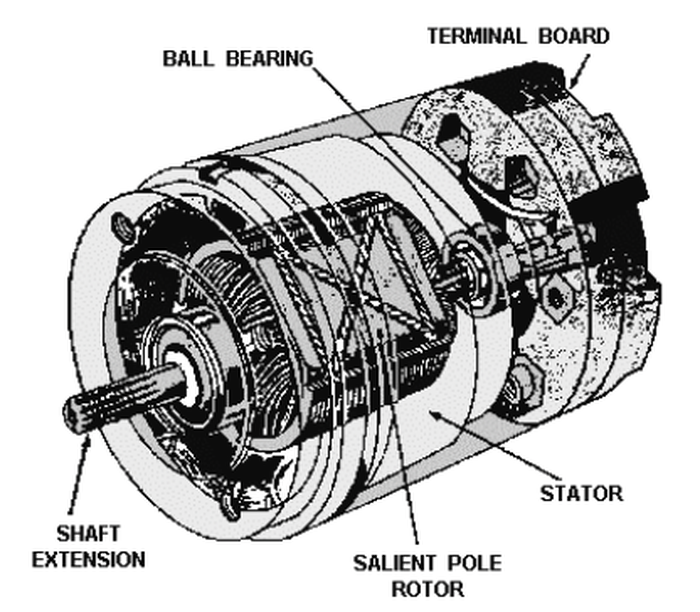
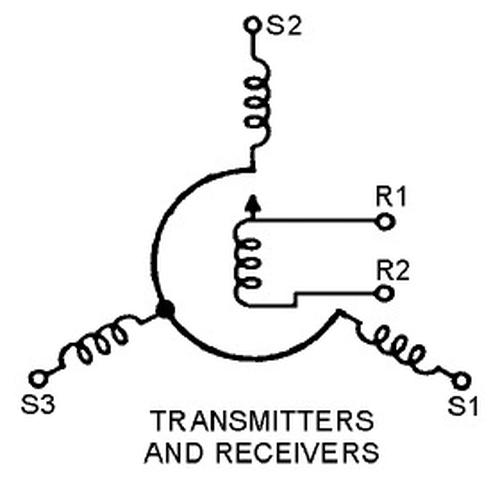
A synchro is an interesting device that can transmit a rotational position electrically over three wires. In appearance, a synchro is similar to an electric motor, but its internal construction is different, as shown below. Before digital systems, synchros were very popular for transmitting signals electrically through an aircraft. For instance, a synchro could transmit an altitude reading to a cockpit display or a targeting system. Two synchros at different locations have their stator windings connected together, while the rotor windings are driven with AC. Rotating the shaft of one synchro causes the other to rotate to the same position.6
For the CADC, most of the outputs are synchro signals, using compact synchros that are about 3 cm in length. For improved resolution, many of the CADC outputs use two synchros: a coarse synchro and a fine synchro. The two synchros are typically geared in an 11:1 ratio, so the fine synchro rotates 11 times as fast as the coarse synchro. Over the output range, the coarse synchro may turn 180°, providing the approximate output unambiguously, while the fine synchro spins multiple times to provide more accuracy.
Examining the Mach section of the CADC
The Bendix CADC is constructed from modular sections. In this blog post, I'm focusing on the middle section, called the "Mach section" and indicated by the arrow above. This section computes log static pressure, impact pressure, pressure ratio, and Mach number and provides these outputs electrically as synchro signals. It also provides the log pressure ratio and log static pressure to the rest of the CADC as shaft rotations. The left section of the CADC computes values related to airspeed, air density, and temperature.7 The right section has the pressure sensors (the black domes), along with the servo mechanisms that control them.
I had feared that any attempt at disassembly would result in tiny gears flying in every direction, but the CADC was designed to be taken apart for maintenance. Thus, I could remove the left section of the CADC for analysis. Unfortunately, we lost the gear alignment between the sections and don't have the calibration instructions, so the CADC no longer produces accurate results.
The diagram below shows the internal components of the Mach section after disassembly. The synchros are in pairs to generate coarse and fine outputs; the coarse synchros can be distinguished because they have spiral anti-backlash springs installed. These springs prevent wobble in the synchro and gear train as the gears change direction. The gears and differentials are not visible from this angle as they are underneath the metal plate. The Pressure Error Correction (PEC) subsystem has a motor to drive the shaft and a control transformer for feedback. The Mach section has two D-sub connectors. The one on the right links the Mach section and pressure section to the front section of the CADC. The Position Error Correction (PEC) servo amplifier board plugs into the left connector. The static pressure and total pressure input lines have fittings so the lines can be disconnected from the lines from the front of the CADC.8
The photo below shows the left section of the CADC. This section meshes with the Mach section shown above. The two sections have parts at various heights, so they join in a complicated way. Two gears receive the pressure signals \( log ~ P_t / P_s \) and \( log ~ P_s \) from the Mach section. The third gear sends the log total temperature to the rest of the CADC. The electrical connector (a standard 37-pin D-sub) supplies 120 V 400 Hz power to the Mach section and pressure transducers and passes synchro signals to the output connectors.
The position error correction servo loop
The CADC receives two pressure inputs and two pressure transducers convert the pressures into rotational positions, providing the indicated static pressure \( P_{si} \) and the total pressure \( P_t \) as shaft rotations to the rest of the CADC. (I explained the pressure transducers in detail in the previous article.)
There's one complication though. The static pressure \( P_s \) is the atmospheric pressure outside the aircraft. The problem is that the static pressure measurement is perturbed by the airflow around the aircraft, so the measured pressure (called the indicated static pressure \( P_{si} \)) doesn't match the real pressure. This is bad because a "static-pressure error manifests itself as errors in indicated airspeed, altitude, and Mach number to the pilot."9
The solution is a correction factor called the Position Error Correction. This factor gives the ratio between the real pressure \( P_s \) and the measured pressure \( P_{si} \). By applying this correction factor to the indicated (i.e. measured) pressure, the true pressure can be obtained. Since this correction factor depends on the shape of the aircraft, it is generated outside the CADC by a separate cylindrical unit called the Compensator, customized to the aircraft type. The position error computation depends on two parameters: the Mach number provided by the CADC and the angle of attack provided by an aircraft sensor. The compensator determines the correction factor by using a three-dimensional cam. The vintage photo below shows the components inside the compensator.
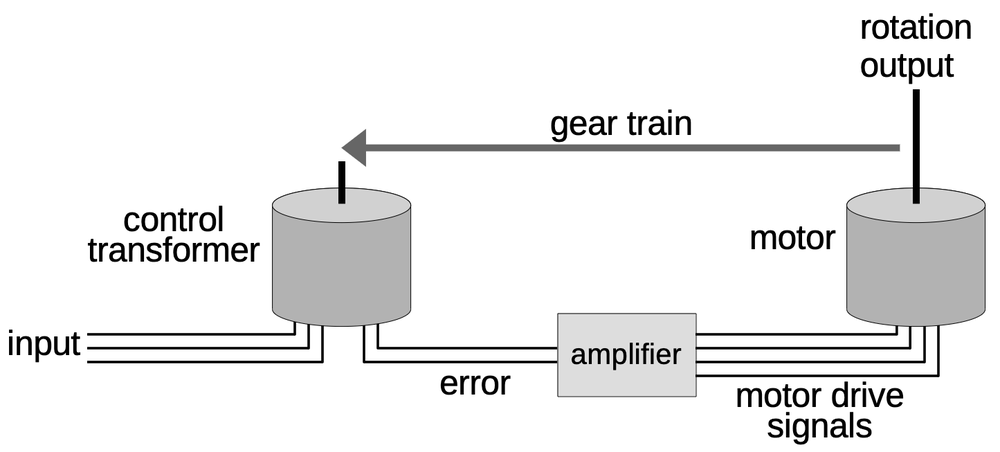
The correction factor is transmitted from the compensator to the CADC as a synchro signal over three wires. To use this value, the CADC must convert the synchro signal to a shaft rotation. The CADC uses a motorized servo loop that rotates the shaft until the shaft position matches the angle specified by the synchro input.
The key to the servo loop is a control transformer. This device looks like a synchro and has five wires like a synchro, but its function is different. Like the synchro motor, the control transformer has three stator wires that provide the angle input. Unlike the synchro, the control transformer also uses the shaft position as an input, while the rotor winding generates an output voltage indicating the error. This output voltage indicates the error between the control transformer's shaft position and the three-wire angle input. The control transformer provides its error signal as a 400 Hz sine wave, with a larger signal indicating more error.10
The amplifier board (below) drives the motor in the appropriate direction to cancel out the error. The power transformer in the upper left is the largest component, powering the amplifier board from the CADC's 115-volt, 400 Hertz aviation power. Below it are two transformer-like components; these are the magnetic amplifiers. The relay in the lower-right corner switches the amplifier into test mode. The rest of the circuitry consists of transistors, resistors, capacitors, and diodes. The construction is completely different from modern printed circuit boards. Instead, the amplifier uses point-to-point wiring between plastic-insulated metal pegs. Both sides of the board have components, with connections between the sides through the metal pegs.
The amplifier board is implemented with a transistor amplifier driving two magnetic amplifiers, which control the motor.11 (Magnetic amplifiers are an old technology that can amplify AC signals, allowing the relatively weak transistor output to control a larger AC output.12) The motor is a "Motor / Tachometer Generator" unit that also generates a voltage based on the motor's speed. This speed signal provides negative feedback, limiting the motor speed as the error becomes smaller and ensuring that the feedback loop doesn't overshoot. The photo below shows how the amplifier board is mounted in the middle of the CADC, behind the static pressure tubing.
The equations
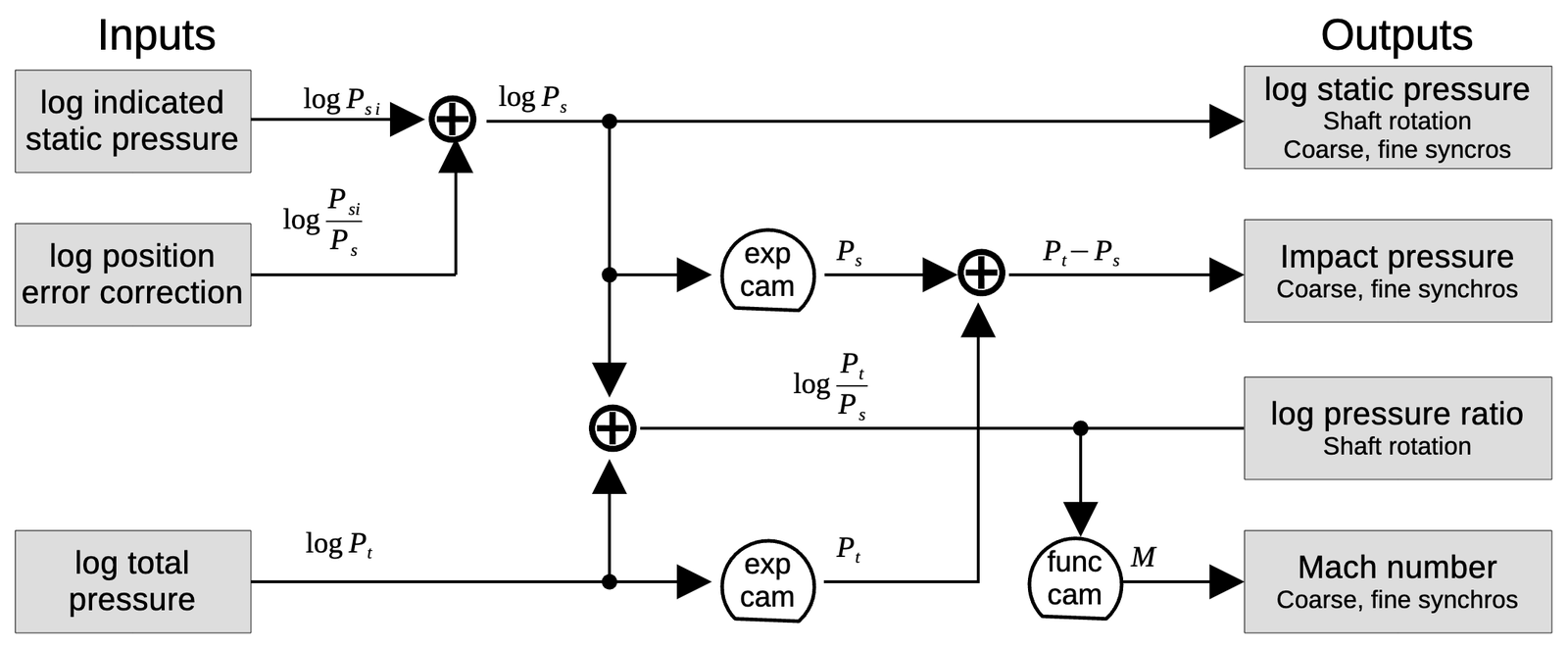
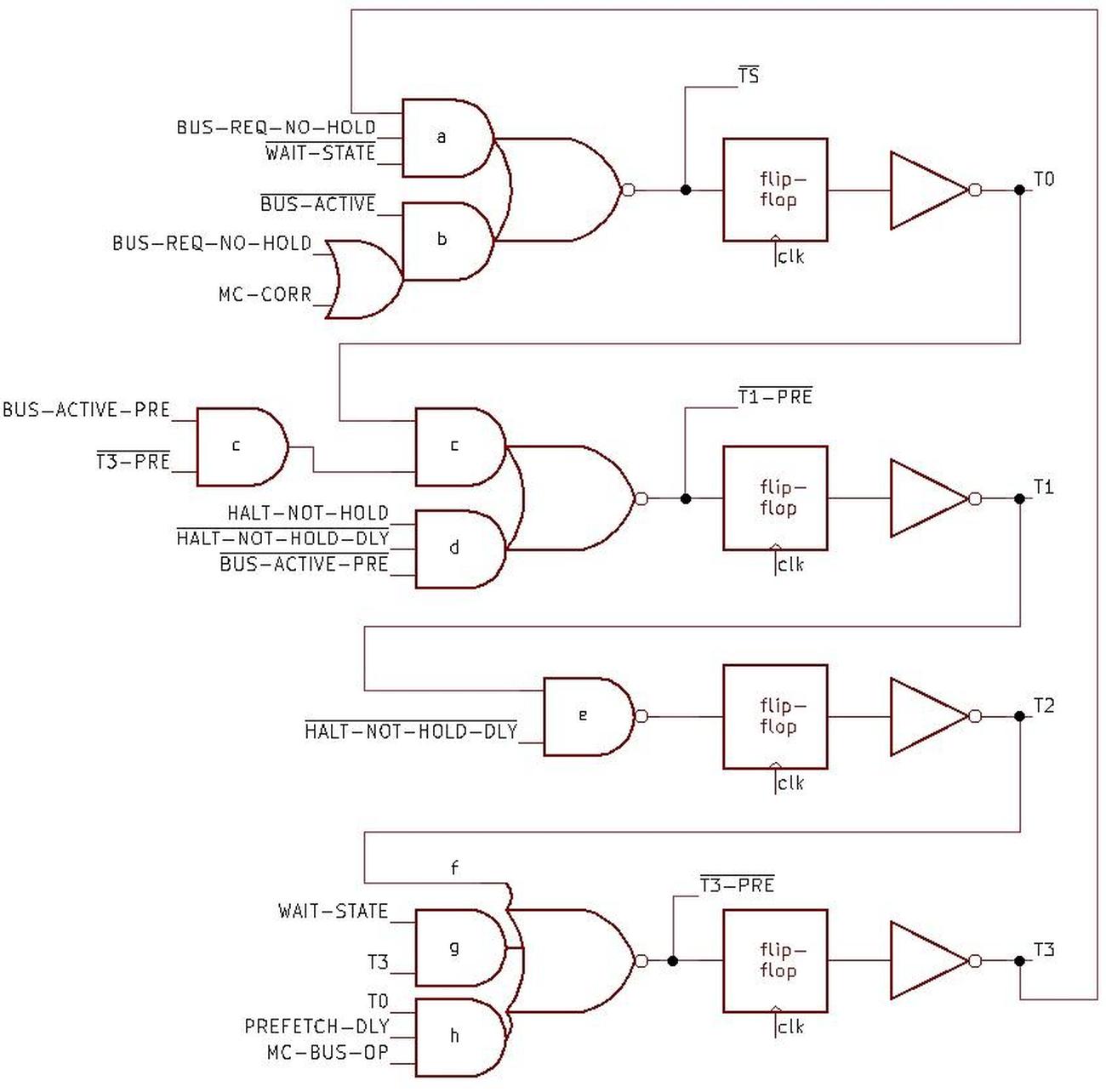
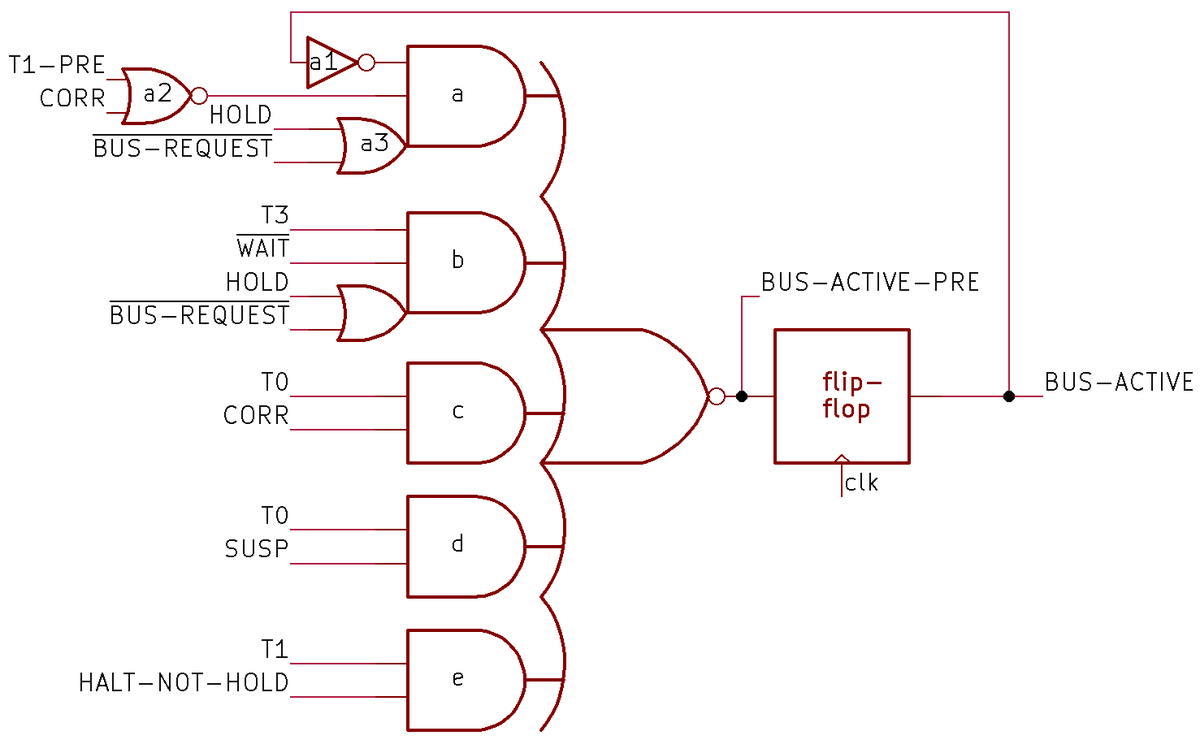
Although the CADC looks like an inscrutable conglomeration of tiny gears, it is possible to trace out the gearing and see exactly how it computes the air data functions. With considerable effort, I have reverse-engineered the mechanisms to create the diagram below, showing how each computation is broken down into mechanical steps. Each line indicates a particular value, specified by a shaft rotation. The ⊕ symbol indicates a differential gear, adding or subtracting its inputs to produce another value. The cam symbol indicates a cam coupled to a differential gear. Each cam computes either a specific function or an exponential, providing the value as a rotation. At the right, the outputs are either shaft rotations to the rest of the CADC or synchro outputs.
I'll go through each calculation briefly.
log static pressure
The static pressure is calculated by dividing the indicated static pressure by the pressure error correction factor. Since these values are all represented logarithmically, the division turns into a subtraction, performed by a differential gear. The output goes to two synchros, geared to provide coarse and fine outputs.13
\[log ~ P_s = log ~ P_{si} - log ~ P_{si} / P_s \]
Impact pressure
The impact pressure is the pressure due to the aircraft's speed, the difference between the total pressure and the static pressure. To compute the impact pressure, the log pressure values are first converted to linear values by exponentiation, performed by cams. The linear pressure values are then subtracted by a differential gear. Finally, the impact pressure is output through two synchros, coarse and fine in an 11:1 ratio.
\[ P_t - P_s = exp(log ~ P_t) - exp(log ~ P_s) \]
log pressure ratio
The log pressure ratio \( P_t/P_s \) is the ratio of total pressure to static pressure. This value is important because it is used to compute the Mach number, true airspeed, and log free air temperature. The Mach number is computed in the Mach section as described below. The true airspeed and log free air temperature are computed in the left section. The left section receives the log pressure ratio as a rotation. Since the left section and Mach section can be separated for maintenance, a direct shaft connection is not used. Instead, each section has a gear and the gears mesh when the sections are joined.
Computing the log pressure ratio is straightforward. Since the log total pressure and log static pressure are both available, subtracting the logs with a differential yields the desired value. That is,
\[log ~ P_t/P_s = log ~ P_t - log ~ P_s \]
Mach number
The Mach number is defined in terms of \(P_t/P_s \), with separate cases for subsonic and supersonic:14
\[M<1:\] \[~~~\frac{P_t}{P_s} = ( 1+.2M^2)^{3.5}\]
\[M > 1:\]
\[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]
Although these equations are very complicated, the solution is a function of one variable \(P_t/P_s\) so M can be computed with a single cam. In other words, the mathematics needed to be done when the CADC was manufactured, but once the cam exists, computing M is easy, using the log pressure ratio computed earlier:
\[ M = f(log ~ P_t / P_s) \]
Conclusions
The CADC performs nonlinear calculations that seem way too complicated to solve with mechanical gearing. But reverse-engineering the mechanism shows how the equations are broken down into steps that can be performed with cams and differentials, using logarithms for multiplication and division. The diagram below shows the complex gearing in the Mach section. Each differential below corresponds to a differential in the earlier equation diagram.
Follow me on Twitter @kenshirriff or RSS for more reverse engineering. I'm also on Mastodon as @oldbytes.space@kenshirriff. Thanks to Joe for providing the CADC. Thanks to Nancy Chen for obtaining a hard-to-find document for me.15 Marc Verdiell and Eric Schlaepfer are working on the CADC with me. CuriousMarc's video shows the CADC in action:
Notes and references
-
My articles on the CADC are:
There is a lot of overlap between the articles, so skip over parts that seem repetitive :-) ↩
-
The static air pressure can also be provided by holes in the side of the pitot tube; this is the typical approach in fighter planes. ↩
-
Multiplying a rotation by a constant factor doesn't require a differential; it can be done simply with the ratio between two gears. (If a large gear rotates a small gear, the small gear rotates faster according to the size ratio.) Adding a constant to a rotation is even easier, just a matter of defining what shaft position indicates 0. For this reason, I will ignore constants in the equations. ↩
-
Strictly speaking, the output of the differential is the sum of the inputs divided by two. I'm ignoring the factor of 2 because the gear ratios can easily cancel it out. It's also arbitrary whether you think of the differential as adding or subtracting, since it depends on which rotation direction is defined as positive. ↩
-
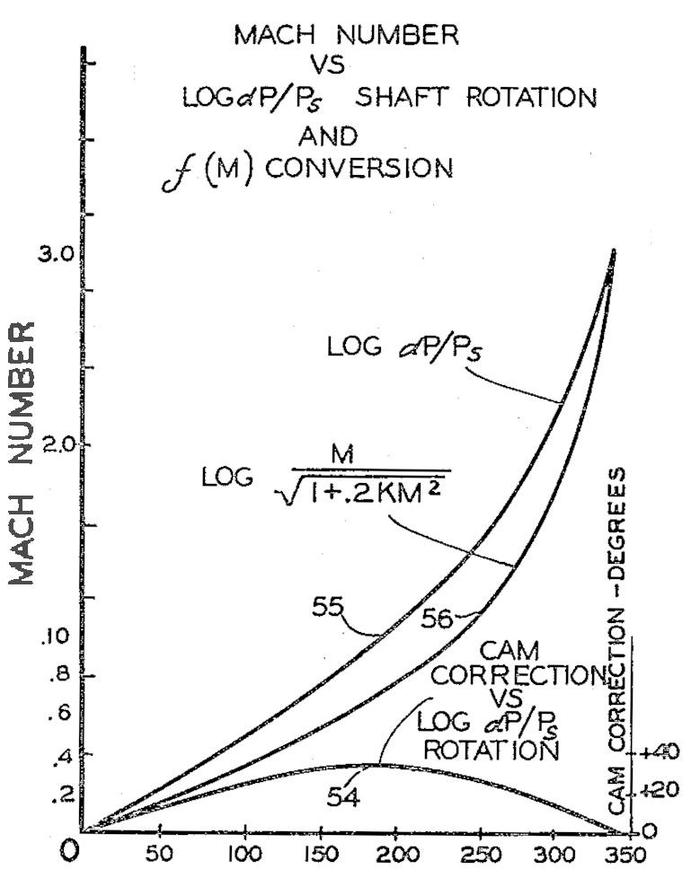
The diagram below shows a typical cam function in more detail. The input is \(log~ dP/P_s\) and the output is \(log~M / \sqrt{1+.2KM^2}\). The small humped curve at the bottom is the cam correction. Although the input and output functions cover a wide range, the difference that is encoded in the cam is much smaller and drops to zero at both ends.
This diagram, from Patent 2969910, shows how a cam implements a complicated function. -
Internally, a synchro has a moving rotor winding and three fixed stator windings. When AC is applied to the rotor, voltages are developed on the stator windings depending on the position of the rotor. These voltages produce a torque that rotates the synchros to the same position. In other words, the rotor receives power (26 V, 400 Hz in this case), while the three stator wires transmit the position. The diagram below shows how a synchro is represented schematically, with rotor and stator coils.
The schematic symbol for a synchro.A control transformer has a similar structure, but the rotor winding provides an output, instead of being powered. ↩
-
Specifically, the left part of the CADC computes true airspeed, air density, total temperature, log true free air temperature, and air density × speed of sound. I discussed the left section in detail here. ↩
-
From the outside, the CADC is a boring black cylinder, with no hint of the complex gearing inside. The CADC is wired to the rest of the aircraft through round military connectors. The front panel interfaces these connectors to the D-sub connectors used internally. The two pressure inputs are the black cylinders at the bottom of the photo.
The exterior of the CADC. It is packaged in a rugged metal cylinder. It is sealed by a soldered metal band, so we needed a blowtorch to open it. -
The concepts of position error correction are described here. ↩
-
The phase of the signal is 0° or 180°, depending on the direction of the error. In other words, the error signal is proportional to the driving AC signal in one direction and flipped when the error is in the other direction. This is important since it indicates which direction the motor should turn. When the error is eliminated, the signal is zero. ↩
-
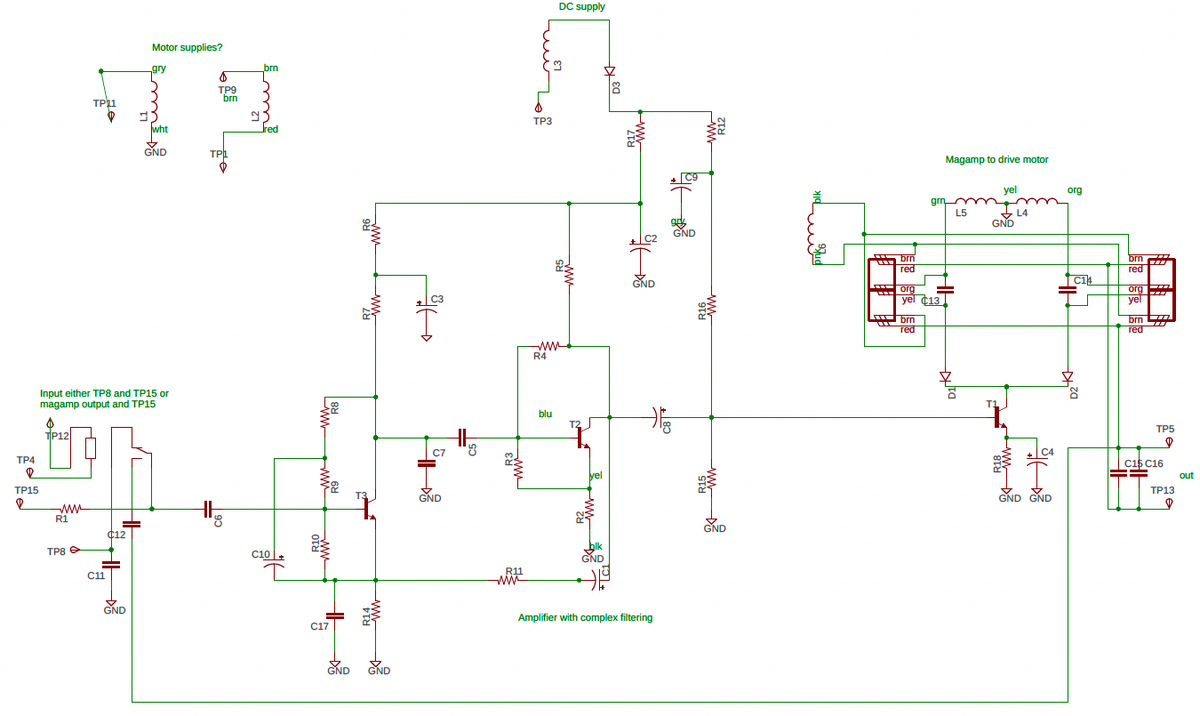
I reverse-engineered the circuit board to create the schematic below for the amplifier. The idea is that one magnetic amplifier or the other is selected, depending on the phase of the error signal, causing the motor to turn counterclockwise or clockwise as needed. To implement this, the magnetic amplifier control windings are connected to opposite phases of the 400 Hz power. The transistor is connected to both magnetic amplifiers through diodes, so current will flow only if the transistor pulls the winding low during the half-cycle that the winding is powered high. Thus, depending on the phase of the transistor output, one winding or the other will be powered, allowing that magnetic amplifier to pass AC to the motor.
This reverse-engineered schematic probably has a few errors. Click the schematic for a larger version.The CADC has four servo amplifiers: this one for pressure error correction, one for temperature, and two for pressure. The amplifiers have different types of inputs: the temperature input is the probe resistance, the pressure error correction uses an error voltage from the control transformer, and the pressure inputs are voltages from the inductive pickups in the sensor. The circuitry is roughly the same for each amplifier—a transistor amplifier driving two magnetic amplifiers—but the details are different. The largest difference is that each pressure transducer amplifier drives two motors (coarse and fine) so each has two transistor stages and four magnetic amplifiers. ↩
-
The basic idea of a magnetic amplifier is a controllable inductor. Normally, the inductor blocks alternating current. But applying a relatively small DC signal to a control winding causes the inductor to saturate, permitting the flow of AC. Since the magnetic amplifier uses a small signal to control a much larger signal, it provides amplification.
In the early 1900s, magnetic amplifiers were used in applications such as dimming lights. Germany improved the technology in World War II, using magnetic amplifiers in ships, rockets, and trains. The magnetic amplifier had a resurgence in the 1950s; the Univac Solid State computer used magnetic amplifiers (rather than vacuum tubes or transistors) as its logic elements. However, improvements in transistors made the magnetic amplifier obsolete except for specialized applications. (See my IEEE Spectrum article on magnetic amplifiers for more history of magnetic amplifiers.) ↩
-
The CADC specification defines how the parameter values correspond to rotation angles of the synchros. For instance, for the log static pressure synchros, the CADC supports the parameter range 0.8099 to 31.0185 inches of mercury. The spec defines the corresponding synchro outputs as 16,320° rotation of the fine synchro and 175.48° rotation of the coarse synchro over this range. The synchro null point corresponds to 29.92 inches of mercury (i.e. zero altitude). The fine synchro is geared to rotate 93 times as fast as the coarse synchro, so it rotates over 45 times during this range, providing higher resolution than a single synchro would provide. The other synchro pairs use a much smaller 11:1 ratio; presumably high accuracy of the static pressure was important. ↩
-
Although the CADC's equations may seem ad hoc, they can be derived from fluid dynamics principles. These equations were standardized in the 1950s by various government organizations including the National Bureau of Standards and NACA (the precursor of NASA). ↩
-
It was very difficult to find information about the CADC. The official military specification is MIL-C-25653C(USAF). After searching everywhere, I was finally able to get a copy from the Technical Reports & Standards unit of the Library of Congress. The other useful document was in an obscure conference proceedings from 1958: "Air Data Computer Mechanization" (Hazen), Symposium on the USAF Flight Control Data Integration Program, Wright Air Dev Center US Air Force, Feb 3-4, 1958, pp 171-194. ↩
Subject: Inside the mechanical Bendix Air Data Computer, part 5: motor/tachometers
The servomotors in the CADC are unlike standard motors. Their name—"Motor-Tachometer Generator" or "Motor and Rate Generator"1—indicates that each unit contains both a motor and a speed sensor. Because the motor and generator use two-phase signals, there are a total of eight colorful wires coming out, many more than a typical motor. Moreover, the direction of the motor can be controlled, unlike typical AC motors. I couldn't find a satisfactory explanation of how these units worked, so I bought one and disassembled it. This article (part 5 of my series on the CADC2) provides a complete teardown of the motor/generator and explain how it works.
The image below shows a closeup of two motors powering one of the pressure signal outputs. Note the bundles of colorful wires to each motor, entering in two locations. At the top, the motors drive complex gear trains. The high-speed motors are geared down by the gear trains to provide much slower rotations with sufficient torque to power the rest of the CADC's mechanisms.
The motor/tachometer that we disassembled is shorter than the ones in the CADC (despite having the same part number), but the principles are the same. We started by removing a small C-clip on the end of the motor and and unscrewing the end plate. The unit is pretty simple mechanically. It has bearings at each end for the rotor shaft. There are four wires for the motor and four wires for the tachometer.3
The rotor (below) has two parts on the shaft. the left part is for the motor and the right drum is for the tachometer. The left part is a squirrel-cage rotor4 for the motor. It consists of conducting bars (light-colored) on an iron core. The conductors are all connected at both ends by the conductive rings at either end. The metal drum on the right is used by the tachometer. Note that there are no electrical connections between the rotor components and the rest of the motor: there are no brushes or slip rings. The interaction between the rotor and the windings in the body of the motor is purely magnetic, as will be explained.
The motor/tachometer contains two cylindrical stators that create the magnetic fields, one for the motor and one for the tachometer. The photo below shows the motor stator inside the unit after removing the tachometer stator. The stators are encased in hard green plastic and tightly pressed inside the unit. In the center, eight metal poles are visible. They direct the magnetic field onto the rotor.
The photo below shows the stator for the tachometer, similar to the stator for the motor. Note the shallow notches that look like black lines in the body on the lower left. These are probably adjustments to the tachometer during manufacturing to compensate for imperfections. The adjustments ensure that the magnetic fields are nulled out so the tachometer returns zero voltage when stationary. The metal plate on top shields the tachometer from the motor's magnetic fields.
The poles and the metal case of the stator look solid, but they are not. Instead, they are formed from a stack of thin laminations. The reason to use laminations instead of solid metal is to reduce eddy currents in the metal. Each lamination is varnished, so it is insulated from its neighbors, preventing the flow of eddy currents.
In the photo below, I removed some of the plastic to show the wire windings underneath. The wires look like bare copper, but they have a very thin layer of varnish to insulate them. There are two sets of windings (orange and blue, or red and black) around alternating metal poles. Note that the wires run along the pole, parallel to the rotor, and then wrap around the pole at the top and bottom, forming oblong coils around each pole.5 This generates a magnetic field through each pole.
The motor
The motor part of the unit is a two-phase induction motor with a squirrel-cage rotor.6 There are no brushes or electrical connections to the rotor, and there are no magnets, so it isn't obvious what makes the rotor rotate. The trick is the "squirrel-cage" rotor, shown below. It consists of metal bars that are connected at the top and bottom by rings. Assume (for now) that the fixed part of the motor, the stator, creates a rotating magnetic field. The important principle is that a changing magnetic field will produce a current in a wire loop.7 As a result, each loop in the squirrel-cage rotor will have an induced current: current will flow up9 the bars facing the north magnetic field and down the south-facing bars, with the rings on the end closing the circuits.
But how does the stator produce a rotating magnetic field? And how do you control the direction of rotation? The next important principle is that current flowing through a wire produces a magnetic field.8 As a result, the currents in the squirrel cage rotor produce a magnetic field perpendicular to the cage. This magnetic field causes the rotor to turn in the same direction as the stator's magnetic field, driving the motor. Because the rotor is powered by the induced currents, the motor is called an induction motor.
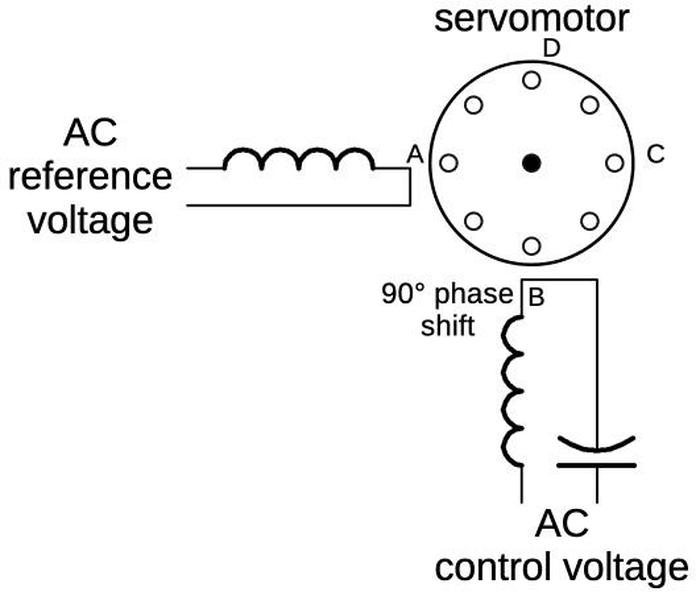
The diagram below shows how the motor is wired, with a control winding and a reference winding. Both windings are powered with AC, but the control voltage either lags the reference winding by 90° or leads the reference winding by 90°, due to the capacitor. Suppose the current through the control winding lags by 90°. First, the reference voltage's sine wave will have a peak, producing the magnetic field's north pole at A. Next (90° later), the control voltage will peak, producing the north pole at B. The reference voltage will go negative, producing a south pole at A and thus a north pole at C. The control voltage will go negative, producing a south pole at B and a north pole at D. This cycle will repeat, with the magnetic field rotating counter-clockwise from A to D. Conversely, if the control voltage leads the reference voltage, the magnetic field will rotate clockwise. This causes the motor to spin in one direction or the other, with the direction controlled by the control voltage. (The motor has four poles for each winding, rather than the one shown below; this increases the torque and reduces the speed.)
The purpose of the capacitor is to provide the 90° phase shift so the reference voltage and the control voltage can be driven from the same single-phase AC supply (in this case, 26 volts, 400 hertz). Switching the polarity of the control voltage reverses the direction of the motor.
There are a few interesting things about induction motors. You might expect that the motor would spin at the same rate as the rotating magnetic field. However, this is not the case. Remember that a changing magnetic field induces the current in the squirrel-cage rotor. If the rotor is spinning at the same rate as the magnetic field, the rotor will encounter an unchanging magnetic field and there will be no current in the bars of the rotor. As a result, the rotor will not generate a magnetic field and there will be no torque to rotate it. The consequence is that the rotor must spin somewhat slower than the magnetic field. This is called "slippage" and is typically a few percent of the full speed, with more slippage as more torque is required.
Many household appliances use induction motors, but how do they generate a rotating magnetic field from a single-phase AC winding? The problem is that the magnetic field in a single AC winding will just flip back and forth, so the motor will not turn in either direction. One solution is a shaded-pole motor, which puts a copper bar around part of each pole to break the symmetry and produce a weakly rotating magnetic field. More powerful induction motors use a startup winding with a capacitor (analogous to the control winding). This winding can either be switched out of the circuit once the motor starts spinning,10 or used continuously, called a permanent-split capacitor (PSC) motor. The best solution is three-phase power (if available); a three-phase winding automatically produces a rotating magnetic field.
Tachometer/generator
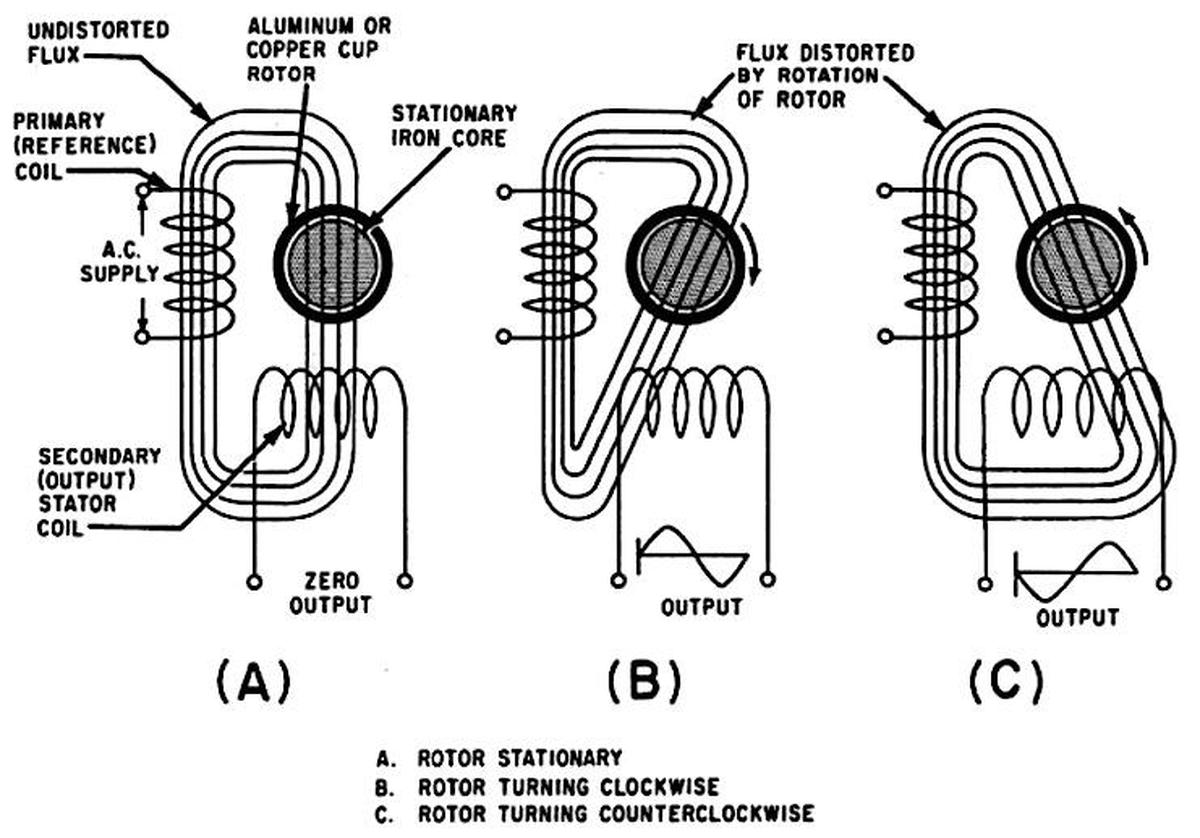
The second part of the unit is the tachometer generator, sometimes called the rate unit.11 The purpose of the generator is to produce a voltage proportional to the speed of the shaft. The unusual thing about this generator is that it produces a 400-hertz output that is either in phase with the input or 180° out of phase. This is important because the phase indicates which direction the shaft is turning. Note that a "normal" generator is different: the output frequency is proportional to the speed.
The diagram below shows the principle behind the generator. It has two stator windings: the reference coil that is powered at 400 Hz, and the output coil that produces the output signal. When the rotor is stationary (A), the magnetic flux is perpendicular to the output coil, so no output voltage is produced. But when the rotor turns (B), eddy currents in the rotor distort the magnetic field. It now couples with the output coil, producing a voltage. As the rotor turns faster, the magnetic field is distorted more, increasing the coupling and thus the output voltage. If the rotor turns in the opposite direction (C), the magnetic field couples with the output coil in the opposite direction, inverting the output phase. (This diagram is more conceptual than realistic, with the coils and flux 90° from their real orientation, so don't take it too seriously. As shown earlier, the coils are perpendicular to the rotor so the real flux lines are completely different.)
But why does the rotating drum change the magnetic field? It's easier to understand by considering a tachometer that uses a squirrel-cage rotor instead of a drum. When the rotor rotates, currents will be induced in the squirrel cage, as described earlier with the motor. These currents, in turn, generate a perpendicular magnetic field, as before. This magnetic field, perpendicular to the orginal field, will be aligned with the output coil and will be picked up. The strength of the induced field (and thus the output voltage) is proportional to the speed, while the direction of the field depends on the direction of rotation. Because the primary coil is excited at 400 hertz, the currents in the squirrel cage and the resulting magnetic field also oscillate at 400 hertz. Thus, the output is at 400 hertz, regardless of the input speed.
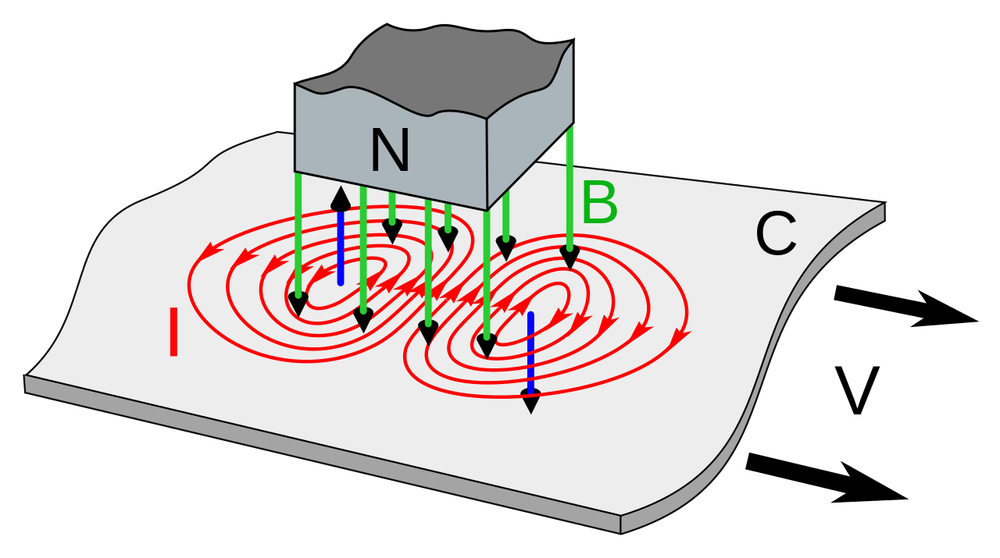
Using a drum instead of a squirrel cage provides higher accuracy because there are no fluctuations due to the discrete bars. The operation is essentially the same, except that the currents pass through the metal of the drum continuously instead of through individual bars. The result is eddy currents in the drum, producing the second magnetic field. The diagram below shows the eddy currents (red lines) from a metal plate moving through a magnetic field (green), producing a second magnetic field (blue arrows). For the rotating drum, the situation is similar except the metal surface is curved, so both field arrows will have a component pointing to the left. This creates the directed magnetic field that produces the output.
The servo loop
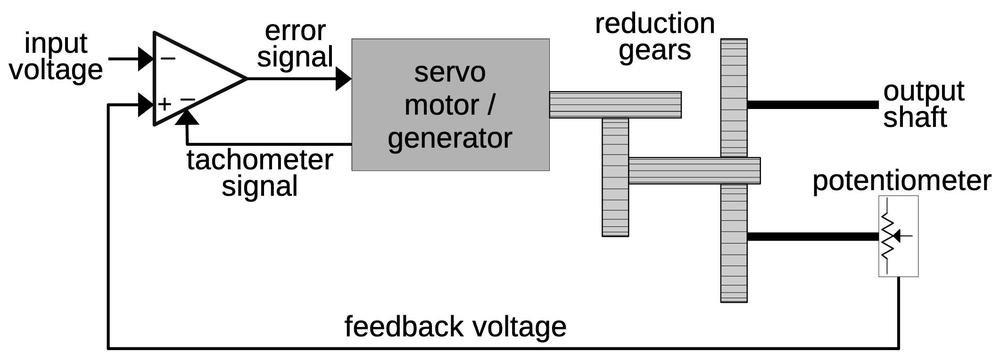
The motor/generator is called a servomotor because it is used in a servo loop, a control system that uses feedback to obtain precise positioning. In particular, the CADC uses the rotational position of shafts to represent various values. The servo loops convert the CADC's inputs (static pressure, dynamic pressure, temperature, and pressure correction) into shaft positions. The rotations of these shafts power the gears, cams, and differentials that perform the computations.
The diagram below shows a typical servo loop in the CADC. The goal is to rotate the output shaft to a position that exactly matches the input voltage. To accomplish this, the output position is converted into a feedback voltage by a potentiometer that rotates as the output shaft rotates.12 The error amplifier compares the input voltage to the feedback voltage and generates an error signal, rotating the servomotor in the appropriate direction. Once the output shaft is in the proper position, the error signal drops to zero and the motor stops. To improve the dynamic response of the servo loop, the tachometer signal is used as a negative feedback voltage. This ensures that the motor slows as the system gets closer to the right position, so the motor doesn't overshoot the position and oscillate. (This is sort of like a PID controller.)
The error amplifier and motor drive circuit for a pressure transducer are shown below. Because of the state of electronics at the time, it took three circuit boards to implement a single servo loop. The amplifier was implemented with germanium transistors (since silicon transistors were later). The transistors weren't powerful enough to drive the motors directly. Instead, magnetic amplifiers (the yellow transformer-like modules at the front) powered the servomotors. The large rectangular capacitors on the right provided the phase shift required for the control voltage.
Conclusions
The Bendix CADC used a variety of electromechanical devices including synchros, control transformers, servo motors, and tachometer generators. These were expensive military-grade components driven by complex electronics. Nowadays, you can get a PWM servo motor for a few dollars with the gearing, feedback, and control circuitry inside the motor housing. These motors are widely used for hobbyist robotics, drones, and other applications. It's amazing that servo motors have gone from specialized avionics hardware to an easy-to-use, inexpensive commodity.
Follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon as @oldbytes.space@kenshirriff. Thanks to Joe for providing the CADC. Thanks to Marc Verdiell for disassembling the motor.
Notes and references
-
The two types of motors in the CADC are part number "FV-101-19-A1" and part number "FV-101-5-A1" (or FV101-5A1). They are called either a "Tachometer Rate Generator" or "Tachometer Motor Generator", with both names applied to the same part number. The "19" and "5" units look the same, with the "19" used for one pressure servo loop and the "5" used everywhere else.
The motor that I got is similar to the ones in the CADC, but shorter. The difference in size is mysterious since both have the Bendix part number FV-101-5-A1.
For reference, the motor I disassembled is labeled:
Cedar Division Control Data Corp. ST10162 Motor Tachometer F0: 26V C0: 26V TACH: 18V 400 CPS DSA-400-70C-4651 FSN6105-581-5331 US BENDIX FV-101-5-A1I wondered why the motor listed both Control Data and Bendix. In 1952, the Cedar Engineering Company was spun off from the Minneapolis Honeywell Regulator Company (better known as Honeywell, the name it took in 1964). Cedar Engineering produced motors, servos, and aircraft actuators. In 1957, Control Data bought Cedar Engineering, which became the Cedar Division of CDC. Then, Control Data acquired Bendix's computer division in 1963. Thus, three companies were involved. ↩
-
My previous articles on the CADC are:
↩ -
From testing the motor, here is how I believe it is wired:
Motor reference (power): red and black
Motor control: blue and orange
Generator reference (power): green and brown
Generator out: white and yellow ↩ -
The bars on the squirrel-cage rotor are at a slight angle. Parallel bars would go in and out of alignment with the stator, causing fluctuations in the force, while the angled bars avoid this problem. ↩
-
This cross-section through the stator shows the windings. On the left, each winding is separated into the parts on either side of the pole. On the right, you can see how the wires loop over from one side of the pole to the other. Note the small circles in the 12 o'clock and 9 o'clock positions: cross sections of the input wires. The individual horizontal wires near the circumference connect alternating windings.
A cross-section of the stator, formed by sanding down the plastic on the end. -
It's hard to find explanations of AC servomotors since they are an old technology. One discussion is in Electromechanical components for servomechanisms (1961). This book points out some interesting things about a servomotor. The stall torque is proportional to the control voltage. Servomotors are generally high-speed, but low-torque devices, heavily geared down. Because of their high speed and their need to change direction, rotational inertia is a problem. Thus, servomotors typically have a long, narrow rotor compared with typical motors. (You can see in the teardown photo that the rotor is long and narrow.) Servomotors are typically designed with many poles (to reduce speed) and smaller air gaps to increase inductance. These small airgaps (e.g. 0.001") require careful manufacturing tolerance, making servomotors a precision part. ↩
-
The principle is Faraday's law of induction: "The electromotive force around a closed path is equal to the negative of the time rate of change of the magnetic flux enclosed by the path." ↩
-
Ampère's law states that "the integral of the magnetizing field H around any closed loop is equal to the sum of the current flowing through the loop." ↩
-
The direction of the current flow (up or down) depends on the direction of rotation. I'm not going to worry about the specific direction of current flow, magnetic flux, and so forth in this article. ↩
-
Once an induction motor is spinning, it can be powered from a single AC phase since the stator is rotating with respect to the magnetic field. This works for the servomotor too. I noticed that once the motor is spinning, it can operate without the control voltage. This isn't the normal way of using the motor, though. ↩
-
A long discussion of tachometers is in the book Electromechanical Components for Servomechanisms (1961). The AC induction-generator tachometer is described starting on page 193.
For a mathematical analysis of the tachometer generator, see Servomechanisms, Section 2, Measurement and Signal Converters, MCP 706-137, U.S. Army. This source also discusses sources of errors in detail. Inexpensive tachometer generators may have an error of 1-2%, while precision devices can have an error of about 0.1%. Accuracy is worse for small airborne generators, though. Since the Bendix CADC uses the tachometer output for damping, not as a signal output, accuracy is less important. ↩
-
Different inputs in the CADC use different feedback mechanisms. The temperature servo uses a potentiometer for feedback. The angle of attack correction uses a synchro control transformer, which generates a voltage based on the angle error. The pressure transducers contain inductive pickups that generate a voltage based on the pressure error. For more details, see my article on the CADC's pressure transducer servo circuits. ↩
Subject: The first microcomputer: The transfluxor-powered Arma Micro Computer from 1962
Obviously, the Arma Micro Computer is not a microcomputer according to modern definitions, since its processor was made from discrete components. But it's an interesting computer in many ways. First, it is an example of the aerospace computers of the 1960s, advanced systems that are now almost entirely forgotten. People think of 1960s computers as room-filling mainframes, but there was a whole separate world of cutting-edge miniaturized aerospace computers. (Taking up just 0.4 cubic feet, the Arma Micro Computer was smaller than an Apple II.) Second, the Arma Micro Computer used strange components such as transfluxors and had an unusual 22-bit serial architecture. Finally, the Arma Micro Computer evolved into a series of computers used on Navy ships and submarines, the E-2C Hawkeye airborne early warning plane, the Concorde, and even Air Force One.
The Arma Micro Computer
The Micro Computer used 22-bit words, which may seem like a strange size from the modern perspective. But there's no inherent need for a word size to be a power of 2. In particular, the Micro Computer was designed for mathematical calculations, not dealing with 8-bit characters. The word size was selected to provide enough accuracy for its navigational tasks.
Another strange aspect of the Micro Computer is that it was a serial machine, sequentially operating on one bit of a word at a time.2 This approach was often used in early machines because it substantially reduced the amount of hardware required: it only needs a 1-bit data bus and a 1-bit ALU. The downside is that a serial machine is much slower because each 22-bit word takes 22 clock cycles (plus 5 cycles of overhead). As a result, the Micro Computer executed just 36000 operations per second, despite its 1 megahertz clock speed.
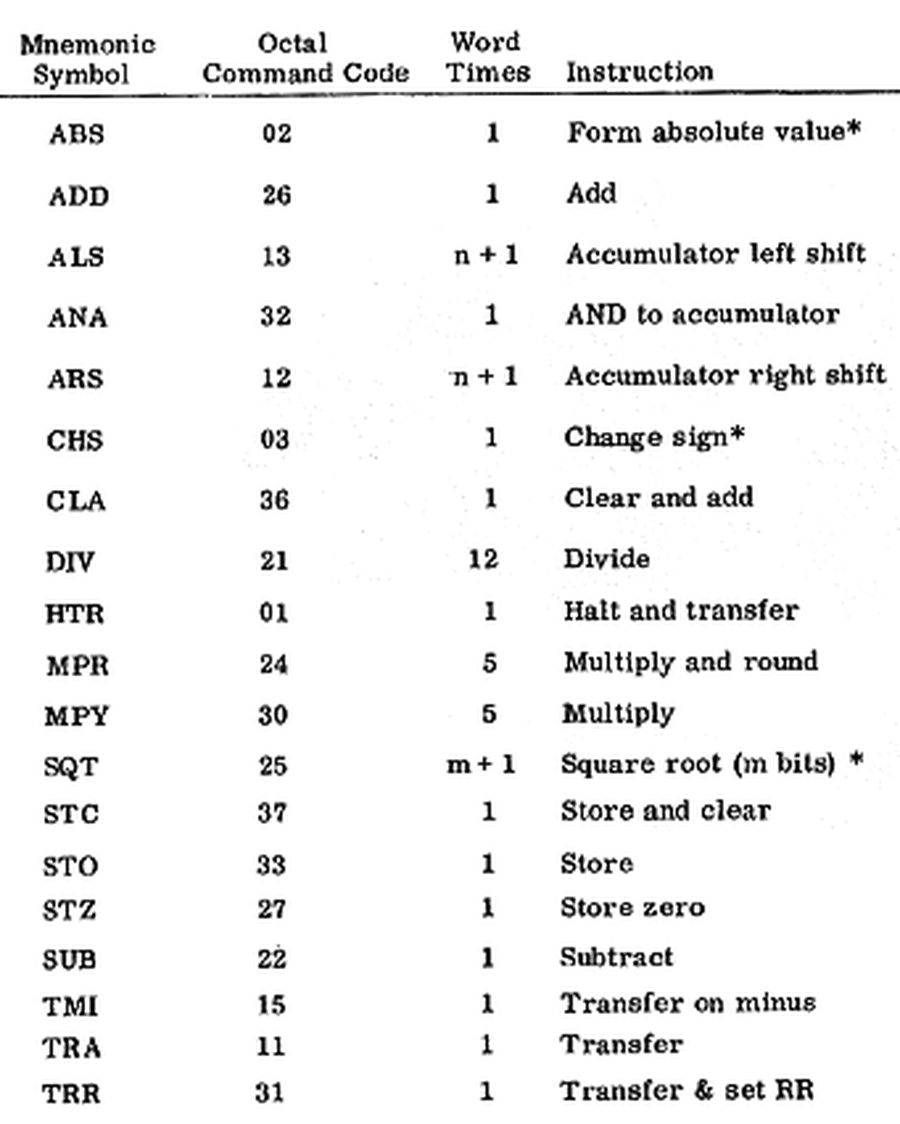
The Micro Computer had a small instruction set of 19 instructions.3 It included multiply, divide, and square root, instructions that weren't implemented in early microprocessors. This illustrates how early microprocessors were a significant step backward in functionality. Moreover, the multiply, divide, and square root instructions used a separate arithmetic unit, so they could execute in parallel with other arithmetic instructions. Because the Micro Computer needed to interact with spacecraft systems, it had a focus on I/O, with 120 digital inputs or outputs, configured as needed for a particular mission.
Circuits
The Micro Computer was built from silicon transistors and diodes, using diode-transistor logic. The construction technique was somewhat unusual. The basic circuits were the flip-flop, the complementary buffer (i.e. an inverter), and the diode gate. Each basic circuit was constructed on a small wafer, .77 inches on a side.5 The photo below shows wafers for a two-transistor flip-flop and two diode gates. Each wafer had up to 16 connection tabs on the edges. These wafers are analogous to integrated circuits, but constructed from discrete components.
The wafers were mounted on printed circuit boards, with up to 22 wafers on a board. Pairs of boards were mounted back to back with polyurethane foam between the boards to form a "sandwich", which was conformally coated. The result was a module that was protected against the harsh environment of a missile or spacecraft. The computer could handle a shock of 100 g's and temperatures of 0°C to 85°C as well as 100% humidity or a vacuum.
Because the Micro Computer was a serial machine, its bits were constantly moving. For register storage such as the accumulator, it used six magnetostrictive torsional delay lines, storing a sequence of bits as physical twists that formed pulses racing through a long coil of wire.
The photo below shows the Arma Micro Computer with the case removed. If you look closely, you can see the 22 small circuit wafers mounted on each printed circuit board. The memory driver boards and delay lines are towards the back, spaced more widely than the other printed circuit boards. The cable harness underneath the boards provides the connections between boards.4
Transfluxors
One of the most unusual parts of the Micro Computer was its storage. Computers at the time typically used magnetic core memory, with each bit stored in a tiny ferrite ring, magnetized either clockwise or counterclockwise to store a 0 or 1. One drawback of standard core memory was that the process of reading a core also cleared the core, requiring data to be written back after a read.
The Micro Computer used ferrite cores, but these were "two-aperture" cores, with a larger hole and a smaller hole, as shown above. Data is written to the "major aperture" and read from the "minor aperture". Although the minor aperture switches state and is erased during a read, the major aperture retains the bit, allowing the minor aperture to be switched back to its original state. Thus, unlike regular core memory, transfluxors don't lose their data when reading.
The resulting system is called non-destructive readout (NDRO), compared to the destructive readout (DRO) of regular core memory.6 The Micro Computer used non-destructive readout memory to ensure that the program memory remained uncorrupted. In contrast, if a program is stored in regular core memory, each instruction must be written back as it is executed, creating the possibility that a transient could corrupt the software. By using transfluxors, this possibility of error is eliminated. (In either case, core memory has the convenient property that data is preserved when power is removed, since data is stored magnetically. With modern semiconductor memory, you lose data when the power goes off.)
The photo below shows a compact transfluxor-based storage module used in the Micro Computer, holding 512 words. In total, the computer could hold up to 7808 words of program memory and 256 words of data memory. It appears that transfluxors didn't live up to their promise, since most computers used regular core memory until semiconductor memory took over in the early 1970s.
Arma's history and the path to the Micro Computer
The Arma Engineering Company was founded in 1918 and built advanced military equipment.7 Its first product was a searchlight for the Navy, followed by a gyroscopic compass and analog computers for naval gun targeting. In 1939, Arma produced the Torpedo Data Computer, a remarkable electromechanical analog computer. US submarines used this computer to track target ships and automatically aim torpedos. The Torpedo Data Computer performed complex trigonometric calculations and integration to account for the motion of the target ship and the submarine. While the Torpedo Data Computer performed well, the Navy's Mark 14 torpedo had many problems—running too deep, exploding too soon, or failing to explode—making torpedoes often ineffectual even with a perfect hit.
Arma underwent major corporate changes due to World War II. Before the war, the German-owned Bosch Company built vehicle starters and aircraft magnetos in the United States. When the US entered World War II in 1941, the government was concerned that a German-controlled company was manufacturing key military hardware so the Office of Alien Property Custodian took over the Bosch plant. In 1948, the banking group that controlled Arma bought Bosch from the Office of the Alien Property Custodian, merging them into the American Bosch Arma Corporation (AMBAC).8 (Arma had earlier received the rights to gyrocompass technology from the German Anschutz company, seized by the Navy after World War I, so Arma benefitted twice from wartime government seizures.)
In the mid-1950s, Arma moved into digital computers, building an inertial guidance computer for the Atlas nuclear missile program. America's first ICBM was the Atlas missile, which became operational in 1959. The first Atlas missiles used radio guidance from the launch site to direct the missile. Since radio signals could be jammed by the enemy, this wasn't a robust solution.
The solution to missile guidance was an inertial navigation system. By using sensitive gyroscopes and accelerometers, a missile could continuously track its position and velocity without any external input, making it unjammable. A key developer of this system was Arma's Wen Tsing Chow, one of the driving forces behind digital aviation computers. He faced extreme skepticism in the 1950s for the idea of putting a computer in a missile. One general mocked him, asking "Where are you going to put the five Harvard professors you'll need to keep it running?" But computerized navigation was successful and in 1961, the Atlas missile was updated to use the Arma inertial guidance computer. It was said to be the first production airborne digital computer.9 Wen Tsing Chow also invented the programmable read-only memory (PROM), allowing missile targeting information to be programmed into a computer outside the factory.
The photo below shows the Atlas ICBM's guidance system. The Arma W-107A computer is at the top and the gyroscopes are in the middle. This computer was an 18-bit serial machine running at 143.36 kHz. It ran a hard-wired program that integrated the accelerometer information and solved equations for the crossrange error function, range error function, and gravity, making these computations every half second.10 The computer weighed 240 pounds and consumed 1000 watts. The computer contained about 36,000 components: discrete transistors, diodes, resistors, and capacitors mounted on 9.5" × 6.5" printed-circuit boards. On the ground, the computer was air-cooled to 55 °F, but there was no cooling after launch as the computer only operated for five minutes of powered flight and wouldn't overheat during that time.
The Atlas wasn't originally designed for a computerized guidance system so there wasn't room inside the missile for the computer. To get around this, a large pod was stuck on the side of the missile to hold the computer and gyroscopes, as indicated in the photo below. This doesn't look aerodynamic, but I guess it worked.
The Atlas guidance computer (left, below) consisted of three aluminum sections called "decks". The top deck held two replaceable target constant units, each providing 54 navigation constants that specified a target. The constants were stored in a stack of printed circuit boards 16" × 8" × 1.5", covered in over a thousand diodes, Wen Tsing Chow's PROM memory. A target was programmed into the stack by a rack of equipment that would selectively burn out diodes, changing the corresponding bit to a 1. (This is why programming a PROM is referred to as "burning the PROM".11) The diode matrix was later replaced with a transfluxor memory array, which had the advantage that it could be reprogrammed as necessary. The top deck also had connectors for the accelerometer inputs, the outputs, and connections for ground support equipment. The bottom deck had power connectors for 28 volts DC and 115V 400 Hz 3-phase AC. In the bottom deck, quartz delay lines were used for storage, representing bits as acoustic waves. Twelve circuit cards, each with a faceted quartz block four inches in diameter, provided a total of 32 words of storage.
Arma considered the Micro Computer the third generation of its airborne computers. The first generation was the Atlas guidance computer, constructed from germanium transistors and diodes (in the pre-silicon era). The second-generation computer moved to silicon transistors and diodes. The third-generation computers still used discrete components, but mounted on the small square wafers. The third generation also had a general-purpose architecture and programmable transfluxor memory instead of a hard-wired program.
After the Micro Computer
Arma continued to develop computers, improving the Arma Micro Computer. The Micro C computer (1965) was developed for Navy ships and submarines. Much like the original Micro, the Micro C used transfluxor storage, but increased the clock frequency to 972 kHz. The computer was much larger: 3.87 cubic feet and 150 pounds. This description states that "the machine is an outgrowth of the ARMA product line of micro computers and is logically and electrically similar to micro-computers designed for missile environments."
In mid-1966, Arma introduced the Micro D computer, built from TTL integrated circuits. Like the original Micro, this computer was serial, but the Micro D had a word length of 18 bits and ran at 1.5 MHz. It weighed 5.25 pounds and was very compact, just 0.09 ft3. Instead of transfluxors, the Micro D used regular magnetic core memory, 4K to 31K words.
The widely-used Litton LTN-51 inertial navigation system was built around the Arma Micro-D computer.12 This navigation system was designed for commercial aircraft, but was also used for military applications, ships, and NASA aircraft. Aircraft from early Concordes to Air Force One used the LTN-51 for navigation. The photo below shows a navigation unit with the Arma Micro-D computer in the lower left and the gyroscope unit on the right.
In early 1968, the Arma Portable Micro D was introduced, a 14-pound battery-powered computer also called the Celestial Data Processor. This handheld computer was designed for navigation in crewed earth orbital flight, determining orbital parameters from stadimeter and sextant measurements performed by astronauts. As far as I can tell, this computer never made it beyond the prototype stage.
Conclusions
The Arma Micro Computer is just one of the dozens of compact aerospace computers of the 1960s, a category that is mostly forgotten and ignored. Another example is the Delco MAGIC I (1961), said to be the "first complete airborne computer to have its logic functions mechanized exclusively with integrated circuits". IBM's 4 Pi series started in 1966 and was used in many systems from the F-15 to the Space Shuttle. By 1968, denser MOS/LSI chips were used in general-purpose aerospace computers such as the Rockwell MOS GP and the Texas Instruments Model 2502 LSI Computer. 13
Arma also illustrates that a company can be on the cutting edge of technology for decades and then suddenly go out of business and be forgotten. After some struggles, Arma was acquired by United Technologies in 1978 for $210 million and was then shut down in 1982. (The German Bosch corporation remains, now a large multinational known for products such as dishwashers, auto parts, and power tools.) Looking at a list of aerospace computers shows many innovative but vanished companies: Univac, Burroughs, Sperry (now all Unisys), AC Electronics (now part of Raytheon), Autonetics (acquired by Boeing), RCA (bought by GE), and TRW (acquired by Northrop Grumman).
Finally, the Micro Computer illustrates that terms such as "microcomputer" are not objective categories but are social constructs. At first, it seems obvious that the Arma Micro Computer is not a real microcomputer. If you consider a microcomputer to be a computer built around a microprocessor, that's true. (Although "microprocessor" is also not as clear as you might think.) But a microcomputer can also be defined as "A small computer that includes one or more input/output units and sufficient memory to execute instructions" (according to the IBM Dictionary of Computing, 1994)14 and the Arma Micro Computer meets that definition. The "microcomputer" is a shifting concept, changing from the 1960s to the 1990s to today.
For more, follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon as @kenshirriff@oldbytes.space. Thanks to Daniel Plotnick for providing a great deal of information and photos. Thanks to John Hartman for obtaining an obscure conference proceedings for me.
Notes and references
-
I should mention the danger of "firsts" from a historical perspective. Historian Michael Williams advised "not to use the word 'first'" and said, "If you add enough adjectives to a description you can always claim your own favorite." (See ENIAC in Action, p7.)
The first usage of "micro-computer" that I could find is from 1956. In Isaac Asimov's short story "The Dying Night", he mentions a "micro-computer" in passing: "In recent years, it [the handheld scanner] had become the hallmark of the scientist, much as the stethoscope was that of the physician and the micro-computer that of the statistician."
Another interesting example of a "micro-computer" is the Texas Instruments Semiconductor Network Computer. This palm-sized computer is often considered the first integrated-circuit computer. It was an 11-bit serial computer running at 100 kHz, built out of RS flip-flops, NOR gates, and logic drivers. The 1961 article below described this computer as a "micro-computer", although this was a one-off use of the term, not the computer's name. This brochure describes the Semiconductor Network Computer in more detail and Semiconductor Networks are described in detail in this article. Unlike modern ICs, these integrated circuits used flying wires for internal connections rather than a deposited metal layer, making their design a dead end.
The Texas Instruments Semiconductor Network Computer. From Computers and Automation, Dec. 1961. -
Most of the information on the Arma Micro Computer in this article is from "The Arma Micro Computer for Space Applications", by E. Keonjian and J. Marx, Spaceborne Computing Engineering Conference, 1962, pages 103-116. ↩
-
The Arma Micro Computer's instruction set consisted of 19 22-bit instructions, shown below.
Instruction set of the Arma Micro Computer. Figure from "The Arma Micro Computer for Space Applications". -
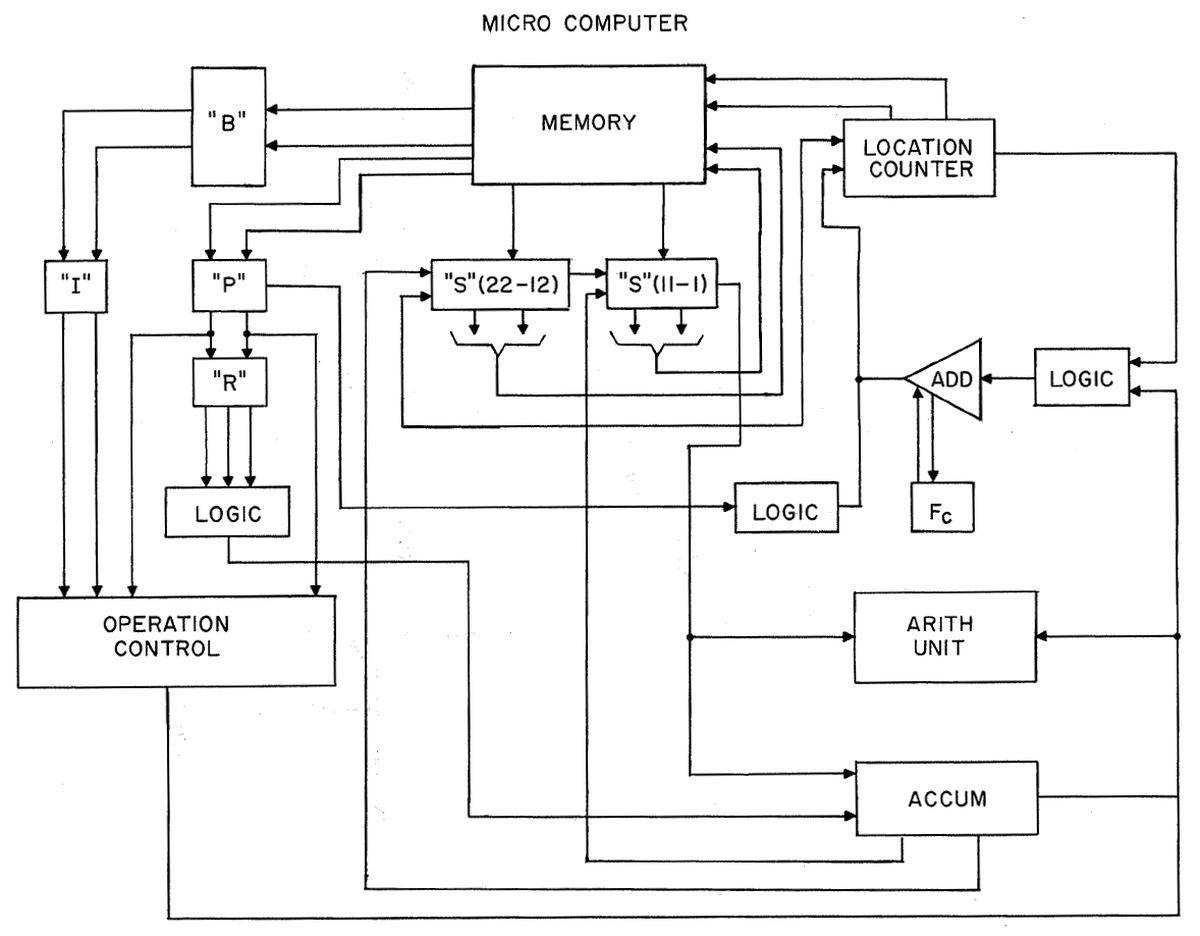
This block diagram shows the structure of the Micro Computer. The accumulator register (AC) is used for all data transfers as well as addition and subtraction. The multiply-divide register is used for multiplication, division, and square roots. The product register (PR), quotient register (QR), and square root register (SR) are used by the corresponding instructions. The data buffer register (S) holds data moving in or out of storage; it is shown with two 11-bit parts.
Block diagram of the Arma Micro Computer. Figure from "The Arma Micro Computer for Space Applications".For control logic, the location counter (L) is the 13-bit program counter. For a subroutine call, the current address can be stored in the recall register (RR), which acts as a link register to hold the return address. (The RR is not shown on the diagram because it is held in memory.) Instruction decoding uses the instruction register (I), with the next instruction in the instruction buffer (B). The operand register (P) contains the 13-bit address from an instruction, while the remaining register (R) is used for I/O addressing. ↩
-
Arma's original plan was to mount circuits on ceramic wafers. Resistors would be printed onto the wafer and wiring silk-screened. (This is similar to IBM's SLT modules (1964), although IBM mounted diode and transistors as bare dies rather than components.) However, the Micro Computer ended up using epoxy-glass wafers with small, but discrete components: standard TO-46 transistors, "fly-speck" diodes, and 1/10 watt resistors. I don't see much advantage to these wafers over mounting the components directly on the printed-circuit board; maybe standardization is the benefit. ↩
-
The Micro Computer used an unusual mechanism to select a word to read or write. Most computers used a grid of selection wires; by energizing an X and a Y wire at the same time, the corresponding core was selected. The key idea of this "coincident-current" approach is that each wire has half the current necessary to flip a core, so the core with the energized X and Y wires will have enough current to flip. This puts tight constraints on the current level, since too much current will flip all the cores along the wire, but not enough current will not flip the selected current. What makes this difficult is that the properties of a core change with temperature, so either the cores need to be temperature-stabilized or the current needs to be adjusted based on the temperature.
The Micro Computer instead used a separate wire for each word, so as long as the current is large enough, the cores will flip. This approach avoids the issues with temperature sensitivity, an important concern for a computer that needs to handle the large temperature swings of a spacecraft, not an air-conditioned data center. Unfortunately, it requires much more wiring. Specifically, the large advantage of the coincident-current approach is that an N×N grid of wires lets you select N2 words. With the Micro Computer approach, N wires only select N words, so the scalability is much worse.
For more on Arma's memory systems, see patents: Memory Device, 3048828 and Multiaperture Core Memory Matrix, 3289181. ↩
-
The capitalization of Arma vs. ARMA is inconsistent. It often appears in all-caps, but both forms are used, sometimes in the same article. "Arma" is not an acronym; the name came from the names of its founders: Arthur Davis and David Mahood (source: Between Human and Machine, p54). I suspect a 1960s corporate branding effort was responsible for the use of all-caps. ↩
-
For more on the corporate history of Arma, see IRE Pulse, March 1958, p9-10. Details of corporate politics and what went wrong are here. More information on the financial ups and downs of Arma is in "Charles Perelle's Spacemanship", Fortune, January 1959, an article that focused on Charles Perelle, the president of American Bosch Arma. ↩
-
Wikipedia says that Arma's guidance computer was "the first production airborne digital computer". However, the Hughes Digitair (1958) has also been called "the first airborne digital computer in actual production." Another source says the Arma computer was the "first all-solid-state, high-reliability, space-borne digital computer." The TRADIC (Transistorized Airborne Digital Computer) (1954) was earlier, but was a prototype system, not a production system. In turn, the TRADIC is said by some to be the first fully transistorized computer, but that depends on exactly how you interpret "fully".
This is another example of how the "first" depends on the specific adjectives used. ↩
-
The information on the Arma W-107A computer is from "Atlas Inertial Guidance System: As I Remember It" by Principal Engineer John Heiderstadt. ↩
-
Chow Wen Tsing's PROM patent discusses the term "burning", explaining that it refers to burning out the diodes electrically. To widen the patent, he clarifies that "The term 'blowing out' or 'burning out' further includes any process which, by means less drastic than actual destruction of the non-linear elements, effects a change of the circuit impedance to a level which makes the particular circuit inoperative." This description prevented someone from trying to get around the patent by stating that nothing was really burning. ↩
-
Details on the LTN-51 navigation system and its uses are in this document. ↩
-
For more information on early aerospace computers, see State-of-the-art of Aerospace Digital Computers (1967), updated as Trends in Aerospace Digital Computer Design (1969). Also see the 1970 Survey of Military CPUs. Efficient partitioning for the batch-fabricated fourth generation computer (1968) discusses how "The computer industry is on the verge of an upheaval" from new hardware including LSI and fast ROMs, and describes various LSI aerospace computers. ↩
-
The "IBM Dictionary of Computing" (1994) has two definitions of "microcomputer": "(1) A digital computer whose processing unit consists of one or more microprocessors, and includes storage and input/output facilities. (2) A small computer that includes one or more input/output units and sufficient memory to execute instructions; for example a personal computer. The essential components of a microcomputer are often contained within a single enclosure." The latter definition was from an ISO/IEC draft standard for terminology so it is somewhat "official". ↩
Subject: The Intel 8088 processor's instruction prefetch circuitry: a look inside
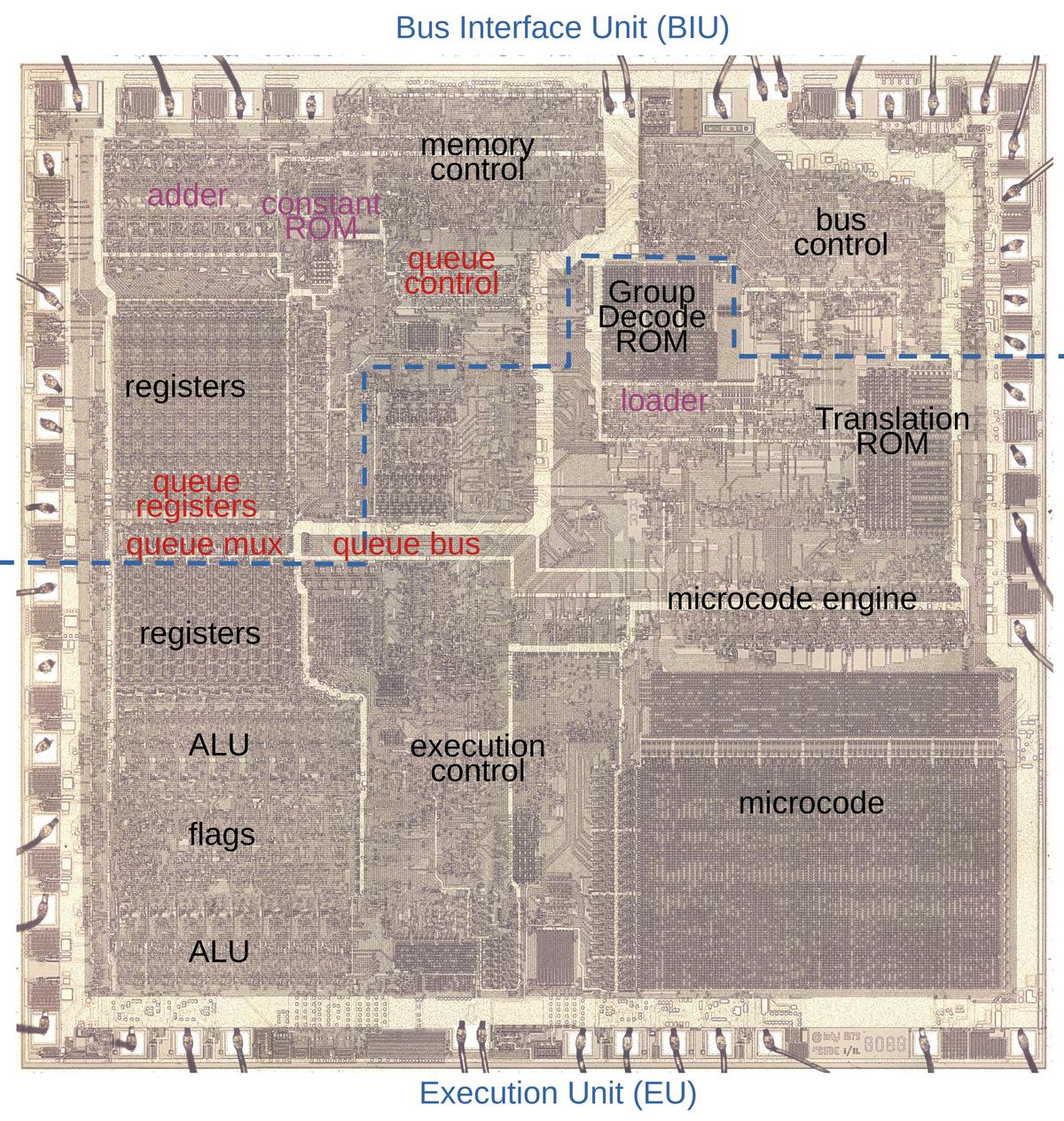
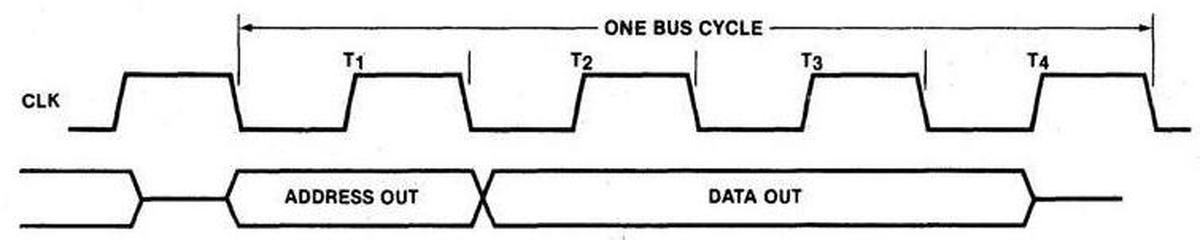
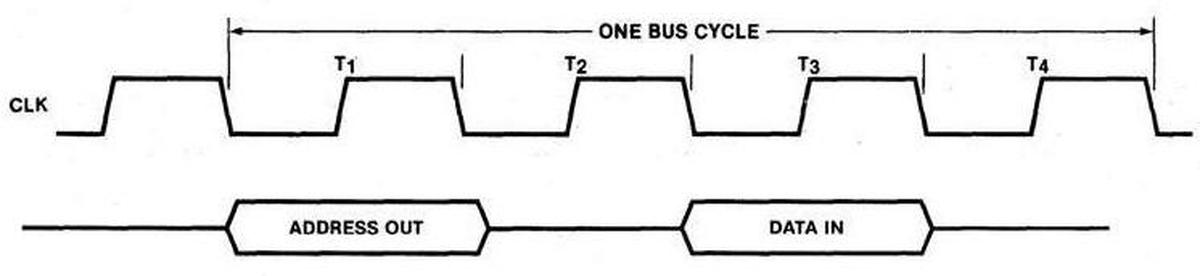
In 1979, Intel introduced the 8088 microprocessor, a variant of the 16-bit 8086 processor. IBM's decision to use the 8088 processor in the IBM PC (1981) was a critical point in computer history, leading to the dominance of the x86 architecture that continues to the present.1 One way that the 8086 and 8088 increased performance was by prefetching: the processor fetches instructions from memory before they are needed, so the processor can execute them without waiting on the relatively slow memory. I've been reverse-engineering the 8088 from die photos and this blog post discusses what I've uncovered about the prefetch circuitry.
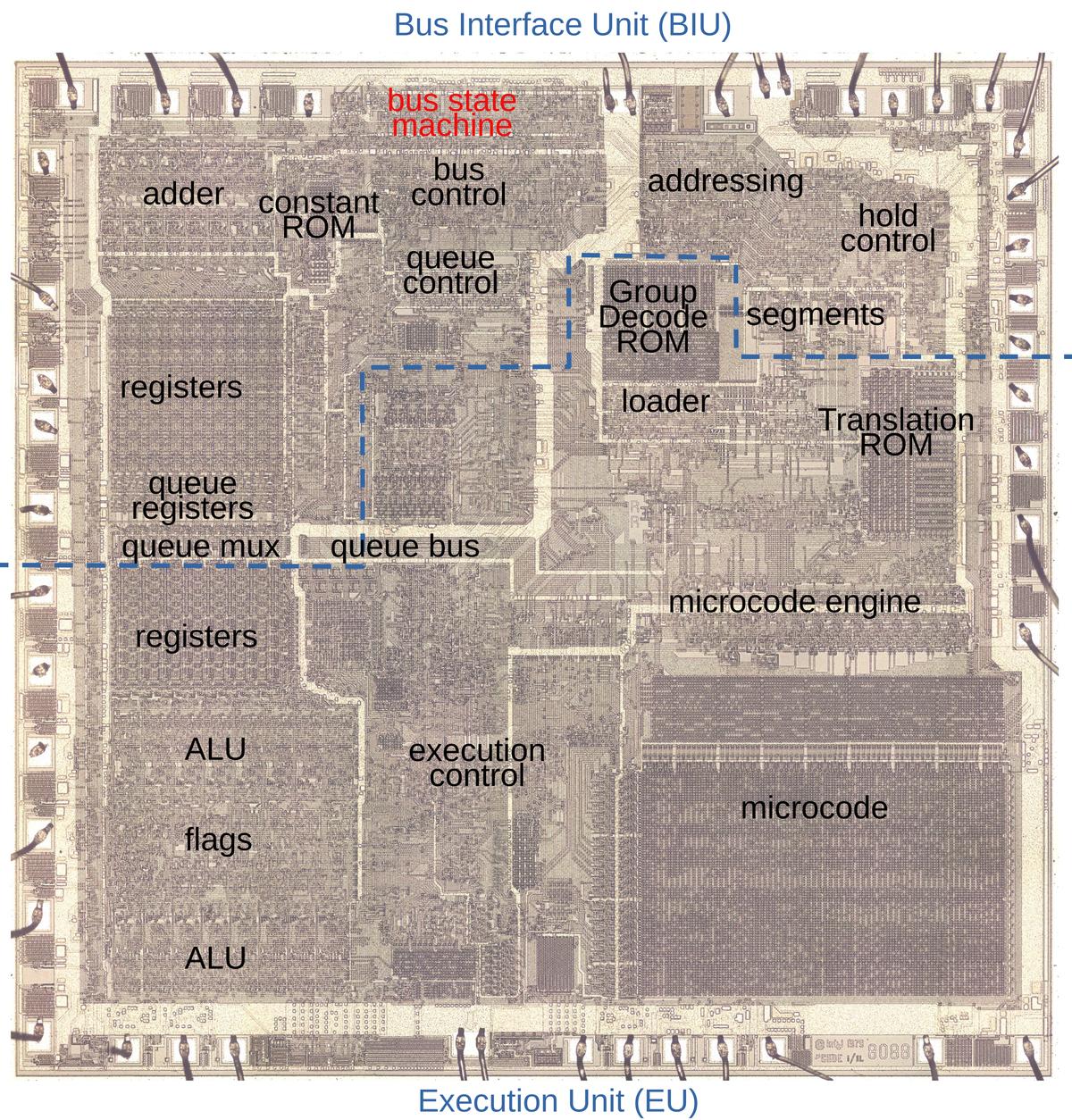
The die photo below shows the 8088 microprocessor under a microscope. The metal layer on top of the chip is visible, with the silicon and polysilicon mostly hidden underneath. Around the edges of the die, bond wires connect pads to the chip's 40 external pins. I've labeled the key functional blocks; this article focuses on the prefetch queue components highlighted in red. The components in purple also play a role, and will be discussed below. Architecturally, the chip is partitioned into a Bus Interface Unit (BIU) at the top and an Execution Unit (EU) below. The BIU handles memory accesses, while the Execution Unit (EU) executes instructions. In particular, the BIU fetches instructions, which are transferred from the prefetch queue to the Execution Unit via the queue bus.
The 8086 and 8088 processors present the same 16-bit architecture to the programmer. The key difference is that the 8088 has an 8-bit data bus for communication with memory and I/O, rather than the 16-bit bus of the 8086. The 8088's narrower bus reduced performance, since the processor only transfers one byte at a time rather than two. However, the 8-bit bus enabled cheaper computer hardware. The 8-bit bus was also a better match for hardware based on the older but popular 8-bit Intel 8080 and 8085 processors, allowing the reuse of 8-bit I/O circuitry for instance. Much of the IBM PC was based on the little-known IBM DataMaster, a computer built around the Intel 8085. Thus, selecting the 8088 processor was a natural choice for the IBM PC.
For the most part, the 8086 and 8088 are very similar internally, apart from trivial but numerous layout changes on the die. The biggest differences are in the Bus Interface Unit, the circuitry that communicates with memory and I/O devices, since this circuitry handles 16 bits in the 8086 versus 8 bits in the 8088. There are a few microcode differences between the two chips. One interesting change is that for performance reasons the 8088 has a smaller prefetch queue than the 8086 (four bytes instead of six). (I wrote about the 8086's prefetch circuity earlier.)
Prefetching and the architecture of the 8086 and 8088
The 8086 and 8088 were introduced at an interesting point in microprocessor history, when memory was becoming slower than the CPU. For the first microprocessors, the speed of the CPU and the speed of memory were comparable.2 However, as processors became faster, the speed of memory failed to keep up. The 8086 was probably the first microprocessor to prefetch instructions to improve performance. While modern microprocessors have megabytes of fast cache3 to act as a buffer between the CPU and much slower main memory, the 8088 has just 4 bytes of prefetch queue. However, this was enough to substantially increase performance.
Prefetching had a major impact on the design of the 8086 and thus the 8088. Earlier processors such as the 6502, 8080, or Z80 were deterministic: the processor fetched an instruction, executed the instruction, and so forth. Memory accesses corresponded directly to instruction fetching and execution and instructions took a predictable number of clock cycles. This all changed with the introduction of the prefetch queue. Memory operations became unlinked from instruction execution since prefetches happen as needed and when the memory bus is available.
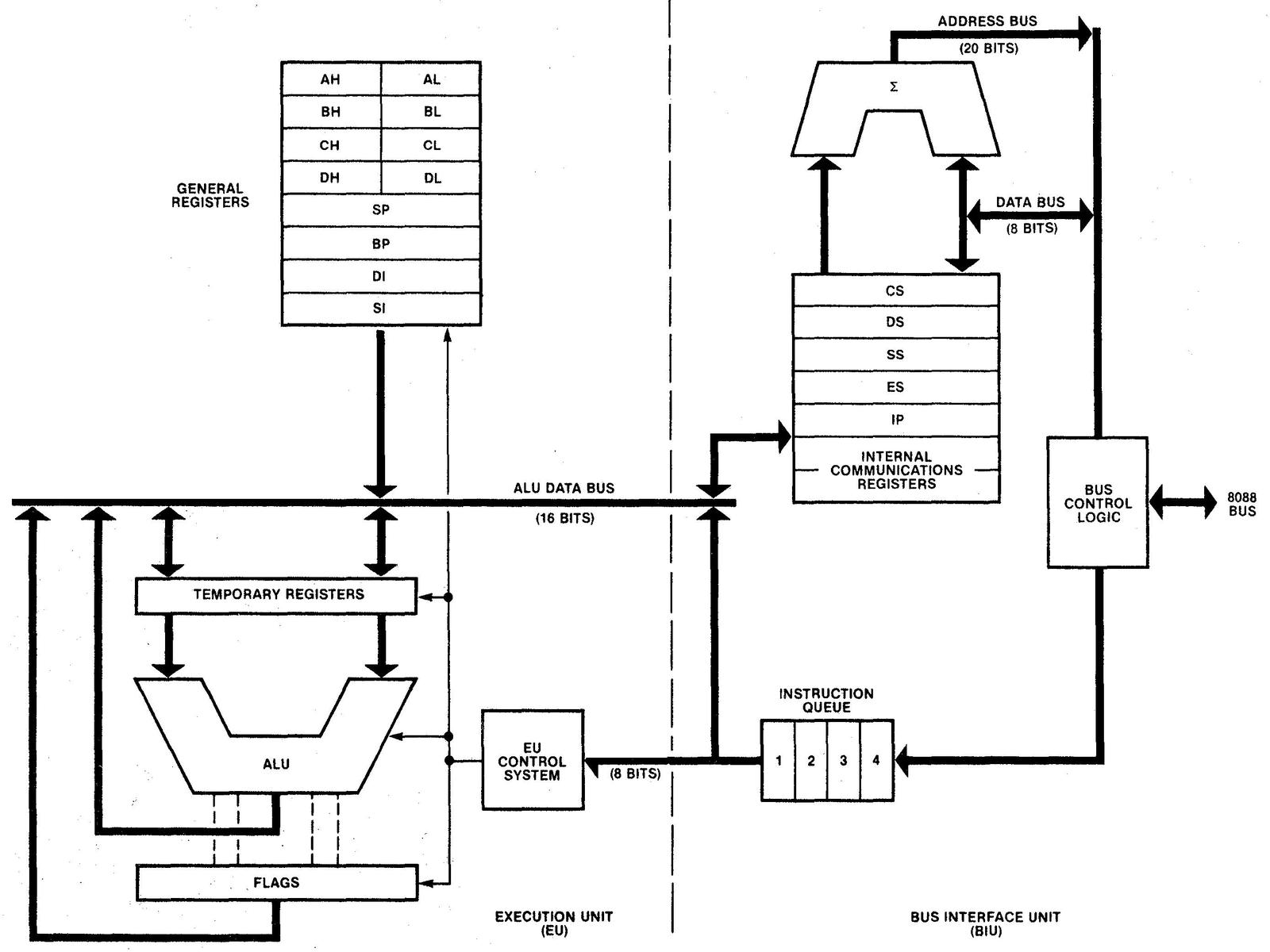
To handle memory operations and instruction execution independently, the implementors of the 8086 and 8088 divided the processors into two processing units: the Bus Interface Unit (BIU) that handles memory accesses, and the Execution Unit (EU) that executes instructions. The Bus Interface Unit contains the instruction prefetch queue; it supplies instructions to the Execution Unit via the Q (queue) bus. The BIU also contains an adder (Σ) for address calculation, adding the segment register base to an address offset, among other things. The Execution Unit is what comes to mind when you think of a processor: it has most of the registers, the arithmetic/logic unit (ALU), and the microcode that implements instructions. The segment registers (CS, DS, SS, ES) and the Instruction Pointer (IP) are in the Bus Interface Unit since they are directly involved in memory accesses, while the general-purpose registers are in the Execution Unit.
It may seem inefficient for the Bus Interface Unit to have its own adder instead of using the ALU, but there are reasons for the separate adder. First, every memory access uses the adder at least once to add the segment base and offset. The adder is also used to increment the PC or index registers. Since these operations are so frequent, they would create a bottleneck if they used the ALU. Second, since the Execution Unit and the Bus Interface Unit run asynchronously with respect to each other, it would be complicated to share the ALU without conflicts.
Prefetching had another major but little-known effect on the 8086 architecture: the designers were considering making the 8086 a two-chip microprocessor. Prefetching, however, required a one-chip design because the number of control signals required to synchronize prefetching across two chips exceeded the package pins available. This became a compelling argument for the one-chip design that was used for the 8086.4 (The unsuccessful Intel iAPX 432, which was under development at the same time, ended up being a two-chip processor: one to fetch and decode instructions, and one to execute them.)
Implementing the queue
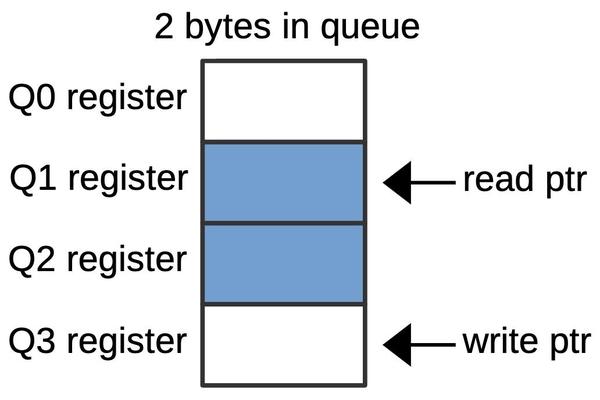
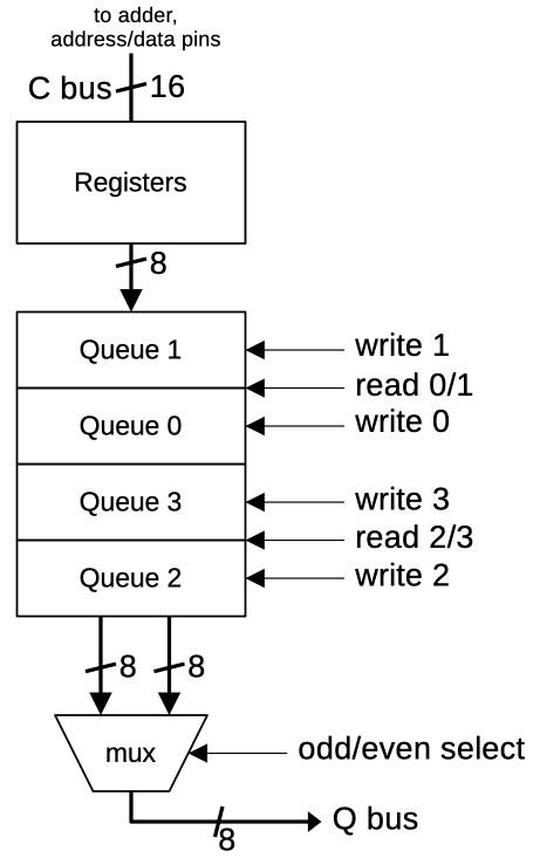
The 8088's instruction prefetch queue is implemented with four 8-bit queue registers along with two hardware "pointers" into the queue. One two-bit counter keeps track of the current read position from 0 to 3, i.e. the queue register that will provide the next instruction byte. The second counter keeps track of the current write position, i.e. the queue register that will receive the next instruction from memory.5 As bytes are fetched from the queue, the read pointer advances. As bytes are added to the queue, the write pointer advances.
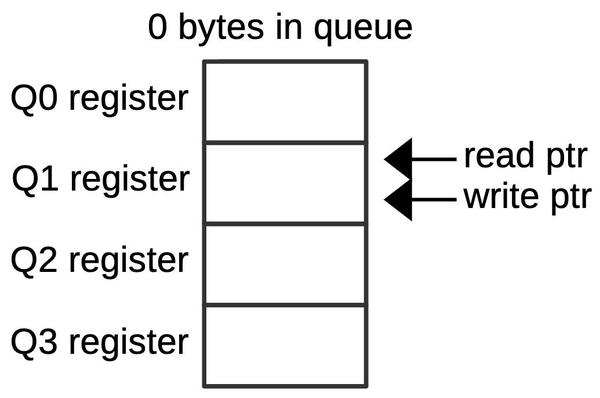
The diagram below shows an example queue configuration with two prefetched bytes. The middle two queue registers (Q1 and Q2) hold data. The read pointer indicates that the Execution Unit will get its next byte from Q1. The write pointer indicates that the next prefetched byte will go into Q3.
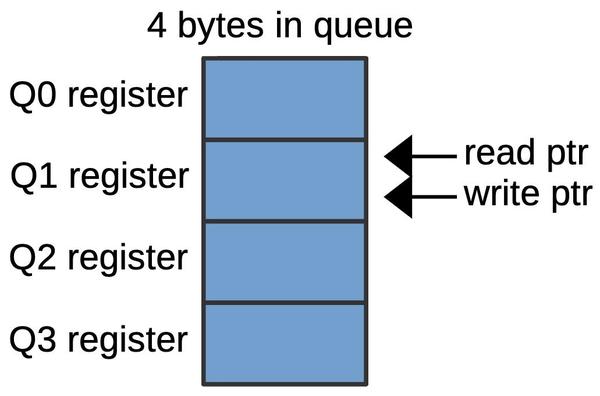
The diagram below shows how the queue pointers can wrap around. In this configuration, two more bytes have been written to the queue (Q3 and Q0), so the queue is full. The write pointer now points to Q1, the same as the read pointer.
There is an important ambiguity, however. Suppose that four bytes are read from the queue, so the read pointer advances four positions, wrapping around back to Q1. The queue is now empty, as shown below, but the pointers have the same position as the full case above. Thus, if the read pointer and the write pointer both point to the same position, the queue may be empty or full. To distinguish these cases, a flip-flop is set if the queue enters the empty state. This flip-flop generates a signal that Intel called MT (empty).
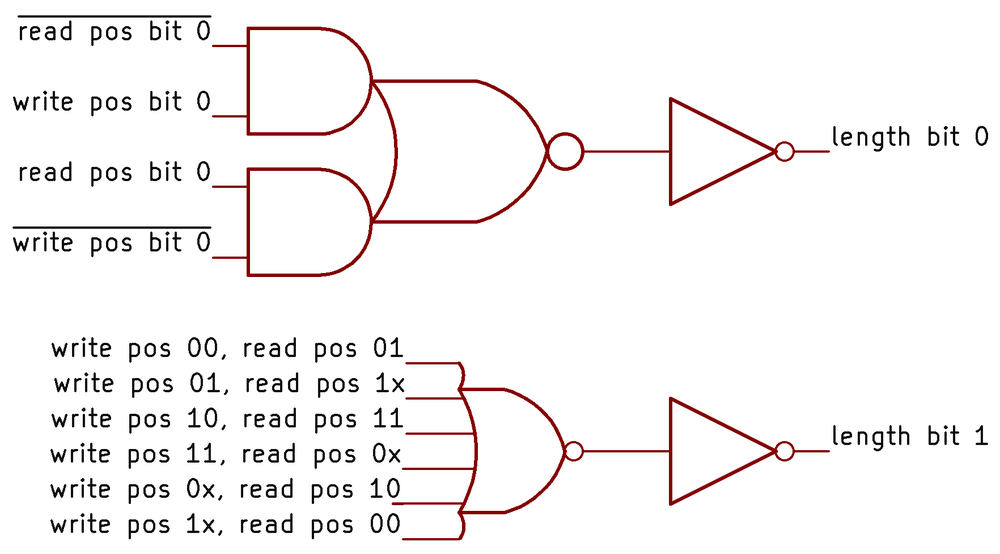
To determine how many bytes are in the queue, the queue circuitry uses a two-bit queue length value, along with the MT flip-flop value to distinguish the empty state. Conceptually, the queue length is generated by subtracting the read position from the write position. However, the implementation does not use a standard subtraction circuit, but instead uses hardcoded logic to determine the two bits of the length, as shown below.
The low bit of the length is the XOR of the two positions. In NMOS logic (used by the 8088), an AND-NOR gate is easy to implement, while an XOR gate is difficult. Thus, XOR is implemented as shown in the top circuit. (You can verify that if one input is 1 and the other is 0, the output is 1.) The high-order bit of the length is also based on an AND-NOR gate, one with six inputs. Each input is a combination of read and write positions that yields an output bit 1; each input is computed by a NOR gate, which I haven't drawn.6 As a result, the amount of logic circuitry to compute the length is fairly large.
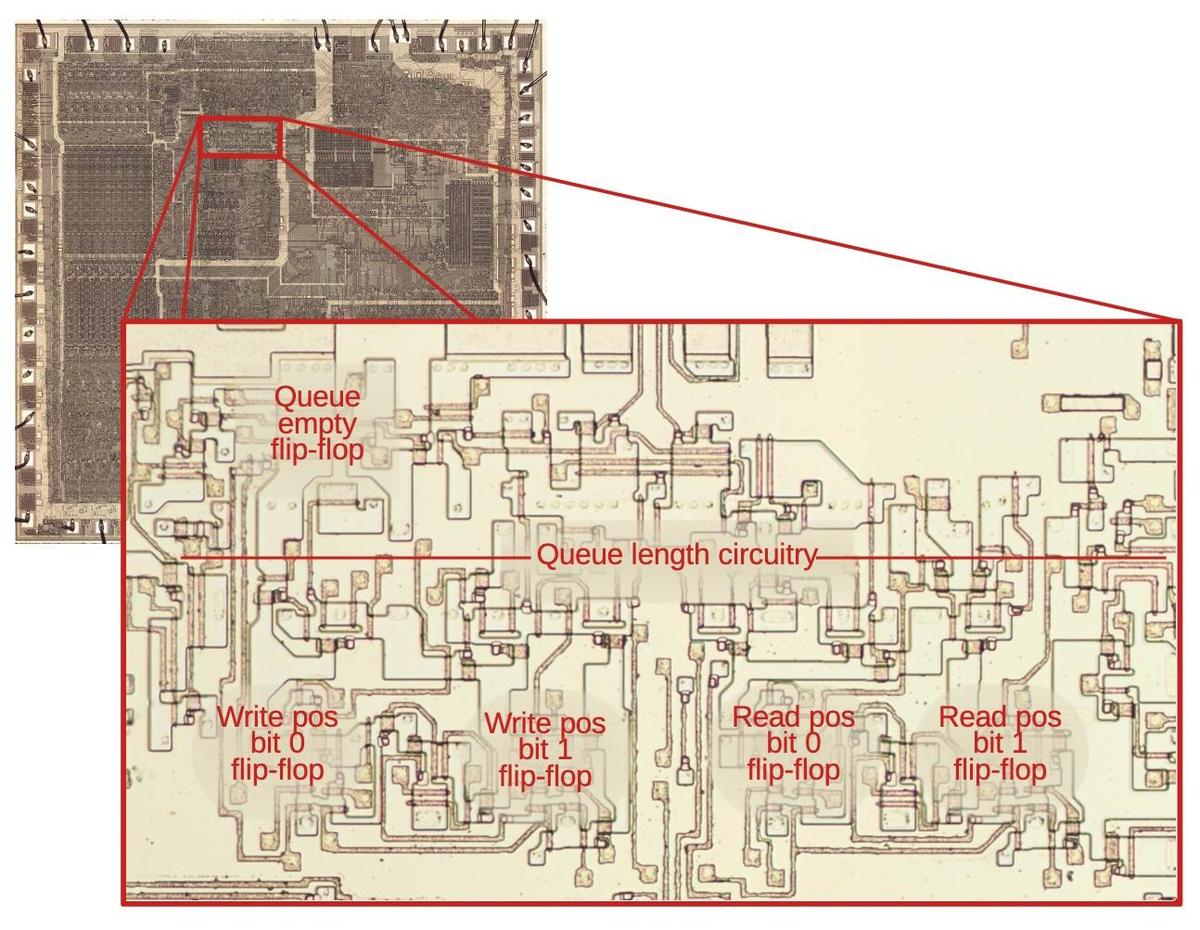
The diagram below zooms in on the queue control circuitry on the die, with the main flip-flops and circuitry labeled. The circuitry in the middle computes the queue length with the 6-input NOR gate stretched across the whole region. The flip-flops for the read and write positions are in the lower region. Despite the relative simplicity of the queue circuits, they take up a substantial part of the die. Compared to modern chips, the density of the 8088 is very low; you can almost see the flip-flops with the naked eye. But this isn't all the circuitry as prefetching also required queue registers and memory cycle control circuitry. Thus, prefetching was a moderately expensive feature for the 8088, as far as die area.
The loader
To decode and execute an instruction, the Execution Unit must get instruction bytes from the Bus Interface Unit, but this is not entirely straightforward. The main problem is that the queue can be empty, in which case instruction decoding must block until a byte is available from the queue. The second problem is that instruction decoding is relatively slow so it is pipelined. For maximum performance, the decoder needs a new byte before the current instruction is finished. A circuit called the "loader" solves these problems by providing synchronization between the prefetch queue and the instruction decoder. The loader uses a small state machine to efficiently fetch bytes from the queue at the right time and to provide timing signals to the decoder and microcode engine.
In more detail, as the loader requests the first two instruction bytes from the prefetch queue, it generates two timing signals that control the microcode execution. The FC (First Clock) indicates that the first instruction byte is available, while the SC (Second Clock) indicates the second instruction byte. Note that the First Clock and Second Clock are not necessarily consecutive clock cycles because the prefetch queue could be empty or contain just one byte, in which case the First Clock and/or Second Clock would be delayed. The instruction decoding circuitry and the microcode engine are controlled by the First Clock and Second Clock signals, so they remain synchronized with the bytes supplied by the prefetch queue.
At the end of a microcode sequence, the Run Next Instruction (RNI) micro-operation causes the loader to fetch the next machine instruction. However, fetching and decoding the next instruction is a bit slow so microcode execution would be blocked for a cycle. In many cases, this slowdown can be avoided: if the microcode knows that it is one micro-instruction away from finishing, it issues a Next-to-last (NXT) micro-operation so the loader can start loading the next instruction. This achieves a degree of pipelining in most cases; fetching the next instruction is overlapped with finishing the execution of the previous instruction.
The diagram above shows the state machine for the loader. I won't explain it in detail, but essentially it keeps track of whether it is waiting for a First Clock byte or a Second Clock byte, and if it is performing a fetch in advance (NXT) or at the end of an instruction (RNI). The state machine is implemented with two flip-flops to support its four states.
Microcode and the prefetch queue
The loader takes care of fetching an instruction that consists of an opcode byte and a Mod R/M (addressing mode) byte. However, many instructions have additional bytes or don't follow this format For example, an opcode such as "ADD AX" can be followed by an 8- or 16-bit immediate value, adding that value to the AX register. Or a "move memory to AX" instruction can be followed by a 16-bit memory address The microcode uses a separate mechanism for fetching these instruction bytes from the queue. Specifically, each micro-instruction contains a source register and a destination register that specify a data move. By specifying "Q" (the queue) as the source, a byte is fetched from the prefetch queue. If the queue is empty, microcode execution blocks until the Bus Interface Unit loads a byte into the prefetch queue. Thus, the complexity of instruction fetching and the prefetch queue is invisible to the microcode.7
A jump, subroutine call, or other control flow change causes the prefetch queue to be flushed since the queue contents
are no longer useful.
This is accomplished in microcode with the FLUSH micro-instruction, which resets the queue read and write pointers and
sets the MT (empty) flip-flop.
Note that the queue is flushed even if the target address is in the queue, for example if you jump one byte ahead.
One complication due to the prefetch queue is that the processor's Instruction Pointer points to the next instruction to
be fetched, not the next instruction to be executed.
This becomes a problem for a subroutine call, which needs to push the return address.
It is also a problem for a relative jump, which is computed from the current instruction.
The solution is the CORR micro-instruction, which corrects the Instruction Pointer by subtracting the queue length to
determine the current execution position.
This is implemented by the Bus Interface Unit, which holds correction constants in the Constant ROM, and subtracts them
using the address adder (not the ALU).8
The queue registers
The 8086 and 8088 partition the registers into upper registers (in the Bus Interface Unit) and lower registers (in the Execution Unit). The upper registers are the registers associated with memory accesses (e.g. Instruction Pointer, segment registers) while the lower registers are more general purpose (e.g. AX, BX, SI, SP). The upper registers are connected to two 16-bit internal buses: the B bus and the C bus.
The queue registers are physically part of the upper registers, but are wired into the buses slightly differently, as shown below. In particular, the 8088's queue registers are written 8 bits at a time from the C bus. (In contrast, the 8086's queue registers can be written 16 bits at a time to support two-byte prefetches.) When accessing the queue, the queue registers are read 16 bits at a time, but only one byte is transferred to the Q bus for instruction processing.9
The diagram below shows how the queue registers appear on the die, comparing the six-byte prefetch queue in the 8086 (top) to the four-byte 8088 queue (bottom). The 8086 prefetch registers are structured as three rows of 16-bit registers, while the 8088 prefetch registers are structured as four rows of 8-bit registers. In both cases, each bit is stored in a cross-coupled pair of inverters. The bit lines (not present) are vertical, while the control lines to select a register are horizontal. The layout is different between the processors to support 16-bit versus 8-bit writes. Note the empty space at the bottom of the 8088 registers. Because the rest of the chips are mostly the same, the 8088 couldn't be "compacted" to avoid this wasted space.
Intel used simulations to determine the best queue sizes for the 8086 and 8088, balancing the performance cost of prefetching against the benefit. (The cost is that prefetching makes the bus unavailable for other memory or I/O operations.) The prefetch queue is discarded on a jump instruction or other change of control flow, causing the prefetched bytes to be wasted. Thus, as the queue gets longer, the chance of discarding a prefetched byte becomes larger, so the potential benefit of prefetching becomes smaller. Since the 8088 prefetches one byte at a time, compared to two bytes at a time on the 8086, prefetching on the 8088 costs twice as much as on the 8086 in terms of bus cycles used per byte. This changes the tradeoffs in favor of a shorter queue.
Because of the difference in queue lengths, the queue control circuitry is different between the 8086 and 8088. In particular, the 8086 needs three-bit counters for the read and write positions, while the 8088 uses two-bit counters. Because of this, the length computation circuitry is also different between the processors.
I plan to continue reverse-engineering the 8088 die so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @oldbytes.space@kenshirriff. If you're interested in the 8086, I wrote about the 8086 die, its die shrink process and the 8086 registers earlier.
Notes and references
-
Whenever I mention x86's domination of the computing market, people bring up ARM, but ARM has a lot more market share in people's minds than in actual numbers. One research firm says that ARM has 15% of the laptop market share in 2023, expected to increase to 25% by 2027. (Surprisingly, Apple only has 90% of the ARM laptop market.) In the server market, just an estimated 8% of CPU shipments in 2023 were ARM. See Arm-based PCs to Nearly Double Market Share by 2027 and Digitimes. (Of course, mobile phones are almost entirely ARM.) ↩
-
Steve Furber, co-creator of the ARM chip, mentions that "The first integrated CPUs were coincidentally quite well matched to semiconductor memory speeds, and were therefore built without caches. This can now be seen as a temporary aberration." See VLSI Risc Architecture and Organization p77. To make this concrete, the Apple II (1977) used a MOS 6502 processor running at about 1 megahertz while its 4116 DRAM chips could perform an access in 250 nanoseconds (4 times the clock speed). The 8088 processor ran at 5-10 MHz which meant that 250 ns DRAM chips were slower than the clock speed. Nowadays, processors run at 4 GHz but DRAM access speed is about 50 nanoseconds (1/200 the clock speed). ↩
-
Modern processors use caches to improve memory performance. Accessing data from a cache is faster than accessing it from main memory, but the tradeoff is that caches are much smaller than main memory. The prefetch queues in the 8086 and 8088 are similar to a cache in some ways, but there are some key differences. First, the prefetch queue is strictly sequential. If you jump ahead two bytes, even if the prefetch queue has those instruction bytes, the processor can't use them. Second, the prefetch queue can't reuse bytes. If you have a 6-byte loop, even though all the code fits in the prefetch queue, it will be reloaded every time. Third, the prefetch queue doesn't provide any consistency. If you modify an instruction in memory a couple of bytes ahead of the PC, the 8086 or 8088 will run the old instruction if it's in the queue. ↩
-
The design decisions for the 8086 prefetch cache (and many other aspects of the chip) are described in: J. McKevitt and J. Bayliss, "New options from big chips," in IEEE Spectrum, vol. 16, no. 3, pp. 28-34, March 1979, doi: 10.1109/MSPEC.1979.6367944. Prefetch provided a 50% performance benefit to the 8086. ↩
-
The queue read process doesn't use an explicit read operation. Instead, the selected queue register continuously puts its value onto the queue bus. When the Execution Unit uses this byte, it sends an increment signal to the queue to advance the read pointer. If the queue empty (MT) flip-flop is set, the Execution Unit will wait until a byte is ready. ↩
-
The NOR gates are used as AND gates, following DeMorgan's laws. For example to produce a 1 output for write position 00 and read position 01, the logic is:
NOR(write bit 1', write bit 0', read bit 1', read bit 0). Note that the bits into the NOR gate are all inverted from the "desired" values; if they are all 0, the NOR output is 1. Thus, there are also some inverters on the inputs. ↩ -
Arbitrary memory reads and writes are performed directly on memory, bypassing the prefetch queue. The 8086/8088 do not provide consistency; if you modify an instruction byte in memory and the byte is in the queue, the processor will execute the old byte. (This type of self-modifying code can be used to determine the queue length, distinguishing the 8086 from the 8088 in software.) ↩
-
The Constant ROM is used for more than just address correction. For example, it is also used to increment the Instruction Pointer after a prefetch. Other constants are used for the 8088's string operations, which act on a block of memory. The index registers are incremented or decremented by 1 for bytes or 2 for words. When popping a value from the stack, the stack pointer is decremented using the Constant ROM. ↩
-
Are the 8088's queue registers 16 bits wide or 8 bits wide? It's ambiguous, since the registers are written 8 bits at a time, but read 16 bits at a time. This implementation was probably selected to support the 8088's 8-bit bus while reusing as much of the 8086 design as possible. In particular, the 8088 can only prefetch one byte at a time, so writes need to happen a byte at a time. Thus, there are four control lines selecting which queue byte is written. (The 8088 could write to half of a 16-bit register but that would require moving the prefetched byte to the correct half of a 16-bit bus.) On the read side, it would make sense to have four read lines, selecting one byte from the 8088's queue. However, since the 8086 already had a multiplexer to select one byte from two, the 8088 designers probably felt it was easier to keep that circuit. And with the smaller queue on the 8088, there was no need to try to save space by removing the circuit. Thus, the queue has two read-select lines and a multiplexer control line. All these lines are controlled by the write position and read position flip-flops. ↩
Subject: Inside an unusual 7400-series chip implemented with a gate array
When I look inside a chip from the popular 7400 series, I know what to expect: a fairly simple die, implemented in a straightforward, cost-effective way. However, when I looked inside a military-grade chip built by Integrated Device Technology (IDT)4 I found a very unexpected layout: over 1500 transistors in an orderly matrix. Even stranger, most of the die is wasted: less than 20% of these transistors are used, forming scattered circuits connected by thin metal wires.
In this blog post, I look at this chip in detail, describe its gates, and explain how it implements the "1-of-4" decoder function. I also discuss why it sometimes makes sense to build chips with a gate array design such as this, despite the inefficiency.
In the photo below, you can see the silicon die in more detail, with the silicon appearing pink. The main circuitry is implemented in the nine rows that form the gate array, a grid of 1584 transistors. The tiny dark rectangles are transistors of two types, NMOS and PMOS, that work together to implement CMOS logic circuits. At this scale, the metal wiring is visible as faint gray lines and smudges, but most of the transistors are unconnected. Surrounding the gate array are 22 input/output (I/O) blocks each with a square bond pad. As with the transistors, many of these I/O blocks are unused. Fourteen of these bond pads have tiny metal bond wires (the thick black lines) that connect the silicon die to the chip's external pins. Finally, the pairs of bond wires at the center left and center right provide ground and power connections for the chip.
The photo below zooms in on three rows of circuitry in the chip. The large dark rectangles are pairs of transistors, with two lines of transistors in each row of circuitry. At the top and bottom of each row, the thick horizontal white lines are metal wiring that provides power and ground. In each row, one line of transistors holds PMOS transistors, next to the power wiring, while the other line holds NMOS transistors, next to the ground wiring. (The orientation flips in each successive row, so it isn't obvious which transistors are which unless you check the power connections at the end of the row.)
The transistors are wired into gates by the metal layers, the white lines. The gates are connected by horizontal and vertical wiring using the wiring channels between the rows. This wiring style is very similar to standard-cell logic. However, unlike standard-cell logic, the underlying transistor grid is fixed, resulting in wasted transistors. In the image above, most of the transistors in the middle row are used, while the top row is unused and the bottom row is mostly unused.
The diagram below shows the structure of one of the transistor blocks, which contains two tall, thin MOS transistors. The vertical metal contacts connect to the sources and drains of the transistors, with the two transistors sharing the middle contact. (On an integrated circuit, the source and drain of a transistor are identical, so it is arbitrary which side is the source and which is the drain.) The short horizontal metal contacts at the top connect to the gates of the two transistors; the gates are made of polysilicon, which is barely visible in the die photo. The gates partition the active silicon (green), forming the transistors. The gate width is approximately 1 µm.
NAND gate
In this section, I'll explain the construction of one of the NAND gates on the die. The NAND gate below uses four transistors, two NMOS transistors on the top and two PMOS transistors on the bottom. The white lines are the metal wiring, forming two layers. Most of the wiring (including power and ground) is in the lower (M1) layer. The slightly wider and darker vertical segments are the upper (M2) layer. The circles connect the metal layers when they join, or connect the metal layer to the underlying silicon or polysilicon. With two metal layers, it's a bit tricky to see how the wiring is connected. The A and B inputs each connect to two transistor gates. The transistor group at the top is connected to ground on the right, with the output on the left. The transistor group on the bottom is connected to Vcc on the left and right, with the output in the middle. This has the effect of putting the upper transistors in series and the lower transistors in parallel.
Below, I've drawn the schematic of the NAND gate. On the left, the layout of the schematic matches the die layout above. On the right, I've redrawn the schematic with a more traditional layout. To understand its operation, note that a PMOS transistor (top on the right schematic) turns on when the input is low, while an NMOS transistor (bottom on the right) turns on when the input is high. When both inputs are high, the two NMOS transistors turn on, connecting ground to the output, pulling it low. When either input is low, one of the PMOS transistors turns on, pulling the output high. Thus, the circuit implements the NAND function. The NMOS and PMOS transistors operate in a complementary fashion, giving CMOS (Complementary MOS) its name.
NOR gate
In this section, I'll explain the layout of one of the NOR gates on the die, shown below.
This gate is twice as large as the previous NAND gate so it can provide twice the output current.1
The NOR gate uses eight transistors, four PMOS transistors in the upper half and four NMOS transistors in the lower half.
(Note that Vcc and ground are flipped compared to the previous gate, as are the NMOS and PMOS transistors.)
The two transistors in each block are wired in parallel to produce more current for
the output.
(A out is the same signal as A in, exiting the block at the top to connect to other circuitry.)
The schematic below shows the wiring of the eight transistors. The schematic layout corresponds to the physical layout to make it easier to map between the image and the schematic. The upper transistor groups are wired in series, while the lower transistor groups are wired in parallel.
The schematic below has been redrawn to make the functionality clearer, and the parallel transistors have been removed. If either input is high, one of the NMOS transistors on the bottom will turn on and pull the input low. If both inputs are low, the two PMOS transistors will turn on and pull the input high. This provides the desired NOR function.
Note that the NAND and NOR gates have similar but opposite schematics. In the NAND gate, the NMOS transistors are in series while the PMOS transistors are in parallel. In the NOR gate, the roles of the transistors are swapped.
The chip's circuit
The chip I examined is a "dual 1-of-4 decoder with enable".2 The decoding function takes a two-bit input and selects one of four output lines depending on the binary value. The enable line must be low to activate this operation; otherwise all four output lines are disabled. The chip contains two of these decoders, which is why it is called a dual decoder. In total, the chip contains 18 logic gates,3 so it is very simple, even by 1990s standards.
I reverse-engineered the chip and created the schematic below, showing one of the dual units.
Each NAND gate matches one of the four input possibilities to drive one of the four outputs.
The NOR gates support the ENABLE signal, blocking the outputs unless ENABLE is active (i.e. low).
The chip uses a general-purpose I/O block (below) for each pin, that can be used as an input or an output depending on how it is wired. Each block contains two large drive transistors: an NMOS transistor to pull the output low and a PMOS transistor to pull the output high. The I/O block has separate control lines for the two output transistors. (At the bottom of the image below, two thin metal wires drive the high-side and low-side transistors.) This permits tri-state logic: if neither transistor is energized, the output is left floating. The gate array drives the output transistors with high-current inverter, constructed from multiple transistors in parallel. (This is why the schematic shows more inverters than may seem necessary.)
When used as an input, the pad is wired to the surrounding circuitry slightly differently, connecting to input protection diodes (not shown on the schematic). Thus, the functionality of the I/O blocks can be changed by modifying the metal layers, without changing the underlying silicon.
Some 7400-series history
The earliest logic integrated circuits used resistors and transistors internally, so they were called RTL (Resistor Transistor Logic), but RTL had significant performance problems. RTL was rapidly replaced by Diode Transistor Logic (DTL) and then Transistor Transistor Logic (TTL). In 1964, Texas Instruments created a line of TTL integrated circuits for military applications called the SN5400 series. This was shortly followed by the commercial-grade SN7400 series.
The 7400 series of integrated circuits was inexpensive, fast, and easy to use. The line started with simple logic circuits such as four NAND gates on a chip, and moved into more complex chips such as counters, shift registers, and ALUs. The 7400 series became very popular in the 1970s and 1980s, used by electronics hobbyists and high-performance minicomputers alike. These chips became essential building blocks and "glue" logic for microcomputers, heavily used in the Apple II for instance.
The original 7400 series branched into dozens of families with different performance characteristics but the same functionality. The 74LS (low-power Schottky) family, for instance, became very popular as it both improved speed and reduced power consumption. In the mid-1970s, 7400-series chips were introduced that used CMOS circuitry instead of TTL for dramatically lower power consumption. This CMOS family, the 74C series, was followed by numerous other CMOS families.
That brings us to the chip I examined, a member of IDT's 74FCT (Fast CMOS TTL-compatible) line of chips, introduced in the mid-1980s. (Specifically, it is in the 54FCT family because it handles a wider temperature range.) These chips used advanced CMOS technology to provide high speed, low power consumption, and as a military option, radiation tolerance.
Conclusions
Why would you make a chip in this inefficient way, using a gate array that wastes most of the die area? The motivation is that most of the design cost can be shared across many different part types. Each step of integrated circuit processing requires an expensive mask for photolithography. With a gate array, all chip types use the same underlying silicon and transistors, with custom masks just for the two metal layers. In comparison, a fully custom chip might require eight custom masks, which costs much more. The tradeoff is that gate array chips are larger so the manufacturing cost is higher per device.5 Thus, a gate array design is better when selling chips in relatively small quantities, while a custom design is cheaper when mass-producing chips.6 IDT focused on the high-performance and military market rather than the commodity chip market, so gate arrays were a good fit.
One last thing. The packaging of this chip is very interesting since it is mounted on a multi-chip module. The module also contains two Atmel EEPROMs. Presumably the decoder chip decodes address bits to select one of the EEPROMs.
Thanks to Don S. for providing the chip. Follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @oldbytes.space@kenshirriff.
Notes and references
-
Properly sizing the transistors in a gate is important for performance. Since the transistors in the gate array are all the same size, multiple transistors are used in parallel to get the desired current. The 1999 book Logical Effort describes a methodology for maximizing the performance of CMOS circuits by correctly sizing the transistors. ↩
-
The part number is "IDT 54FCT139ALB". "54" indicates the chip operates under an enhanced temperature range of -55°C to +125°C. The "A" indicates the chip is 35% faster than the base series (but not as fast as "C"). "L" indicates the chip is packaged in a leadless chip carrier, the square package shown at the top of the article. Finally, "B" indicates the chip was tested according to military standards: MIL-STD-883, Class B. ↩
-
The chip contains 18 logic gates according to the functional schematic in the datasheet (below). The implementation actually uses 52 logic gates by my count (2×26) because the implementation doesn't exactly match the schematic. In particular, the datasheet shows three-input NAND gates, but the chip uses a NAND gate and a NOR gate along with inverters. The chip also has additional inverters to drive the output transistors in each I/O block.
Schematic of the chip from the datasheet. -
Integrated Device Technology was a spinoff from Hewlett Packard that started in 1980. IDT built advanced CMOS chips including fast static RAM and microprocessors (bit-slice and MIPS). It became part of Renesas in 2018. A very detailed 1986 profile of IDT is here. IDT's logo is pretty cool, combining a chip wafer and calculus.
The logo of Integrated Device Technology.Here's how the logo looks on the die:
Closeup of the die showing the IDT logo.The die also has the initials of the designers, along with some mysterious symbols. One looks like the Chinese character "正".
Closeups of two parts of the die. -
Integrated circuit manufacturing is partitioned into the "front end of line", where the transistors are created on the silicon wafer, and the "back end of line", where the metal wiring is put on top to connect the transistors. With a gate array construction, the front end of line steps create generic gate array wafers. The back end of line steps then connect the transistors as desired for a particular component. The gate array wafers can be produced in large quantities and stored, and then customized for specific products in smaller quantities as needed. This reduces the time to supply a particular chip type since only the back end of line process needs to take place. ↩
-
The IDT High-Speed CMOS Logic Design Guide briefly mentions the gate array design. The FCT family was built from two sizes of gate arrays, "4004" for smaller chips and "8000" for larger chips. Later, IDT shrunk the original "Z-step" gate arrays to smaller, higher-performance "Y-step" arrays. They then customized some of the devices to create the "W-step" devices. Looking at the markings on the die, we see that this chip uses the "4004Y" gate array.
The die shows gate slice 4004Y and part 4139Y (indicating 54139 or 74139). The numbers are slightly obscured by a bond wire.
Subject: Talking to memory: Inside the Intel 8088 processor's bus interface state machine
In 1979, Intel introduced the 8088 microprocessor, a variant of the 16-bit 8086 processor. IBM's decision to use the 8088 processor in the IBM PC (1981) was a critical point in computer history, leading to the success of the x86 architecture. The designers of the IBM PC selected the 8088 for multiple reasons, but a key factor was that the 8088 processor's 8-bit bus was similar to the bus of the 8085 processor.1 The designers were familiar with the 8085 since they had selected it for the IBM System/23 Datamaster, a now-forgotten desktop computer, making the more-powerful 8088 processor an easy choice for the IBM PC.
The 8088 processor communicates over the bus with memory and I/O devices through a highly-structured sequence of steps called "T-states." A typical 8088 bus cycle consists of four T-states, with one T-state per clock cycle. Although a four-step bus cycle may sound straightforward, its implementation uses a complicated state machine making it one of the most difficult parts of the 8088 to explain. First, the 8088 has many special cases that complicate the bus cycle. Moreover, the bus cycle is really six steps, with two undocumented "extra" steps to make bus operations more efficient. Finally, the complexity of the bus cycle is largely arbitrary, a consequence of Intel's attempts to make the 8088's bus backward-compatible with the earlier 8080 and 8085 processors. However, investigating the bus cycle circuitry in detail provides insight into the timing of the processor's instructions. In addition, this circuitry illustrates the tradeoffs and implementation decisions that are necessary in a production processor. In this blog post, I look in detail at the circuitry that implements this state machine.
By examining the die of the 8088 microprocessor, I could reverse engineer the bus circuitry. The die photo below shows the 8088 microprocessor's silicon die under a microscope. Most visible in the photo is the metal layer on top of the chip, with the silicon and polysilicon mostly hidden underneath. Around the edges of the die, bond wires connect pads to the chip's 40 external pins. Architecturally, the chip is partitioned into a Bus Interface Unit (BIU) at the top and an Execution Unit (EU) below, with the two units running largely independently. The BIU handles bus communication (memory and I/O accesses), while the Execution Unit (EU) executes instructions. In the diagram, I've labeled the processor's key functional blocks. This article focuses on the bus state machine, highlighted in red, but other parts of the Bus Interface Unit will also play a role.
Although I'm focusing on the 8088 processor in this blog post, the 8086 is mostly the same. The 8086 and 8088 processors present the same 16-bit architecture to the programmer. The key difference is that the 8088 has an 8-bit data bus for communication with memory and I/O, rather than the 16-bit bus of the 8086. For the most part, the 8086 and 8088 are very similar internally, apart from trivial but numerous layout changes on the die. In this article, I'm focusing on the 8088 processor, but most of the description applies to the 8086 as well. Instead of constantly saying "8086/8088", I'll refer to the 8088 and try to point out places where the 8086 is different.
The bus cycle
In this section, I'll describe the basic four-step bus cycles that the 8088 performs.2
To start, the diagram below shows the states for a write cycle (slightly simplified3), when the 8088 writes to memory or an I/O device.
The external bus activity is organized as four "T-states", each one clock cycle long and called T1, T2, T3, and T4, with
specific actions during each state.
During T1, the 8088 outputs the address on the pins. During the T2, T3, and T4 states, the 8088 outputs the data word on the same pins.
The external memory or I/O device uses the T states to know when it is receiving address information or data over the bus lines.
For a read, the bus cycle is slightly different from the write cycle, but uses the same four T-states.
During T1, the address is provided on the pins, the same as for a write.
After that, however, the processor's data pins are "tri-stated" so they float electrically, allowing the external memory to put data on the bus.
The processor reads the data at the end of the T3 state.
The purpose of the bus state machine is to move through these four T states for a read or a write. This process may seem straightforward, but (as is usually the case with the 8088) many complications make this process anything but easy. In the next sections, I'll discuss these complications. After that, I'll explain the state machine circuitry with a schematic.
Address calculation
One of the notable (if not hated) features of the 8088 processor is segmentation: the processor supports 1 megabyte of memory, but memory is partitioned into segments of 64 KB for compatibility with the earlier 8080 and 8085 processors. The 8088 calculates each 20-bit memory address by adding the value of a segment register to a 16-bit offset. This calculation is done by a dedicated address adder in the Bus Interface Unit, completely separate from the chip's ALU. (This address adder can be spotted in the upper left of the earlier die photo.)
Calculating the memory address complicates the bus cycle. As the timing diagrams above show, the processor issues the memory address during state T1 of the bus cycle.
However, it takes time to perform the address calculation addition, so the address calculation must take place
before T1.
To accomplish this, there are two "invisible" bus states before T1; I call these states "TS" (T-start) and "T0".
During these states, the Bus Interface Unit uses the address adder to compute the address, so the address will be available
during the T1 state.
These states are invisible to the external circuitry because they don't affect the signals from the chip.
Thus, a single memory operation takes six clock cycles: two preparatory cycles to compute the address before the four visible cycles.
However, if multiple memory operations are performed, the operations are overlapped to achieve a degree of pipelining that improves performance.
Specifically, the address calculation for the next memory operation takes place during the last two clock cycles of the current
memory operation, saving two clock cycles.
That is, for consecutive bus cycles, T3 and T4 of one bus cycle overlap with TS and T0 of the next cycle.
In other words, during T3 and T4 of one bus cycle, the memory address gets computed for the next bus cycle.
This pipelining significantly improves the performance of the 8088, compared to taking 6 clock cycles for each bus cycle.
With this timing, the address adder is free during cycles T1 and T2.
To improve performance in another way, the 8088 uses the adder during this idle time to increment or decrement memory addresses.
For instance, after popping a word from the stack, the stack pointer needs to be incremented by 2.5
Another case is block move operations (string operations), which need to increment or decrement the pointers each step.
By using the address adder, the new pointer value is calculated "for free" as part of the memory
cycle, without using the processors regular ALU.4
Address corrections
The address adder is used in one more context: correcting the Instruction Pointer value. Conceptually, the Instruction Pointer (or Program Counter) register points to the next instruction to execute. However, since the 8088 prefetches instructions, the Instruction Pointer indicates the next instruction to be fetched. Thus, the Instruction Pointer typically runs ahead of the "real" value. For the most part, this doesn't matter. This discrepancy becomes an issue, though, for a subroutine call, which needs to push the return address. It is also an issue for a relative branch, which jumps to an address relative to the current execution position.
To support instructions that need the next instruction address, the 8088 implements a micro-instruction CORR, which corrects the Instruction Pointer.
This micro-instruction subtracts the length of the prefetch queue from the Instruction Pointer to determine the "real" Instruction Pointer.
This subtraction is performed by the address adder, using correction constants that are stored in a small Constant ROM.
The tricky part is ensuring that using the address adder for correction doesn't conflict with other uses of the adder.
The solution is to run a special shortened memory cycle—just the
TS and T0 states—while the CORR micro-instruction is performed.6
These states block a regular memory cycle from starting, preventing a conflict over the address adder.
Prefetching
The 8088 prefetches instructions before they are needed, loading instructions from memory into a 6-byte prefetch queue.
Prefetching usually improves performance, but can result in an
instruction's memory access being delayed by a prefetch, hurting overall performance.
To minimize this delay, a bus request from an instruction will preempt a prefetch, even if the prefetch has
gone through TS and T0.
At that point, the prefetch hasn't created any bus activity yet (which first happens in T1), so preempting the prefetch
can be done cleanly.
To preempt the prefetch, the bus cycle state machine jumps back to TS, skipping over T1 through T4, and starting the desired access.
A prefetch will also be preempted by the micro-instruction that stops prefetching (SUSP) or the micro-instruction
that corrects addresses (CORR). In these cases, there is no point in completing the prefetch, so the state machine cycle
will end with T0.
Wait states
One problem with memory accesses is that the memory may be slower than the system's clock speed, a characteristic of less-expensive
memory chips.
The solution in the 1970s was "wait states".
If the memory couldn't respond fast enough, it would tell the processor to add idle clock cycles called wait states, until
the memory could respond.7
To produce a wait state, the memory (or I/O device) lowers the processor's READY pin until it is ready to proceed.
During this time, the Bus Interface Unit waits, although the Execution Unit continues operation if possible.
Although Intel's documentation gives the wait cycle a separate name (Tw), internally the wait is implemented by repeating the T3 state as long as the READY pin is not active.
Halts
Another complication is that the 8088 has a HALT instruction that halts program execution until an interrupt comes in.
One consequence is that HALT stops bus operations (specifically prefetching, since stopping execution will automatically stop instruction-driven bus operations).
A complication is that the 8088 indicates the HALT state to external devices by performing a special T1 bus cycle
without any following bus cycles.
But wait: there's another complication. External devices can take control of the bus through the HOLD functionality,
allowing external devices to perform operations such as DMA (Direct Memory Access).
When the device ends the HOLD, the 8088 performs another special T1
bus cycle, indicating that the HALT is still in effect.
Thus, the bus state machine must generate these special T1 states based on HALT and HOLD actions.
(I discussed the HALT process in detail here.)
Putting it all together: the state diagram
The state diagram below summarizes the different types of bus cycles.
Each circle indicates a specific T-state, and the arrows indicate the transitions between states.
The green line shows the basic bus cycle or cycles, starting in TS and then going around the cycle.
From T3, a new cycle can start with T0 or the cycle will end with T4.
Thus, new cycles can start every four clocks, but a full cycle takes six states (counting the "invisible" TS and T0).
The brown line shows that the bus cycle will stay in T3 as long as there is a wait state.
The red line shows the two cycles for a CORR correction, while the purple line shows the special T1 state for a HALT
instruction.
The cyan line shows that a prefetch cycle can be preempted after T0; the cycle will either restart at TS or end.
I'm showing states TS and T3 together since they overlap but aren't the same.
Likewise, I'm showing T4 and T0 together. T4 is grayed out because it doesn't exist from the state machine's perspective;
the circuitry doesn't take any particular action during T4.
The schematic below shows the implementation of the state machine.
The four flip-flops represent the four states, with one flip-flop active at a time, generating states T0, T1, T2,
and T3 (from top to bottom).
Each output feeds into the logic for the next state, with T3 wrapping back to the top, so the circuit moves through
the states in sequence.
The flip-flops are clocked so the active state will move from one flip-flop to the next according to the system clock.
State TS doesn't have its own flip-flop, but is represented by the input to the T0 flip-flop, so it happens one clock
cycle earlier.8
State T4 doesn't have a flip-flop since it isn't "real" to the bus state machine.
The logic gates handle the special cases: blocking the state transfer if necessary or starting a state.
I'll explain the logic for each state in more detail.
The circuitry for the TS state has two AND gates to generate new bus cycles starting from TS.
The first one (a) causes TS to happen with T3 if there is a pending bus request (and no HOLD). The second AND gate (b) starts a bus cycle if
the bus is not currently active and there is a bus request or a CORR micro-instruction.
The flip-flop causes T0 to follow T3/TS, one clock cycle later.
The next gates (c) generate the T1 state following T0 if there is pending bus activity and the cycle isn't preempted to T3. The AND gate (d)
starts the special T1 for the HALT instruction.9
The T2 state follows T1 unless T1 was generated by a HALT (e).
The T3 logic is more complicated. First, T3 will always follow T2 (f).
Next, a wait state will cause T3 to remain in T3 (g).
Finally, for a preempt, T3 will follow T0 (h) if there is a prefetch and a microcode bus operation (i.e. an instruction specified the bus operation).
Next, I'll explain BUS-ACTIVE, an important signal that indicates if the bus is active or not.
The Bus Interface Unit generates the BUS-ACTIVE signal to help control the state machine.
The BUS-ACTIVE signal is also widely used in the Bus Interface Unit, controlling many functions such as transfers to and from
the address registers.
BUS-ACTIVE is generated by the complex circuit below that determines if the bus will be active,
specifically in states T0 through T3.
Because of the flip-flop, the computation of BUS-ACTIVE happens in the previous clock cycle.
In more detail, the signal BUS-ACTIVE-PRE indicates if the bus cycle will continue or will end on the next clock cycle.
Delaying this signal through the flip-flop generates BUS-ACTIVE, which indicates if the bus is currently active in states T0 through T3.
The top AND gate (a) is responsible for starting a cycle or keeping a cycle going (a1).
It will allow a new cycle if there is a bus request (without HOLD) (a3).
It will also allow a new cycle if there is a CORR micro-instruction prior to the T1 state (even if there is a HOLD, since
this "fake" cycle won't use the bus) (a2).
Finally, it allows a new cycle for a HALT, using T1-pre (a2).10
Next are the special cases that end a bus cycle.
The second AND gate (b) ends the bus cycle after T3 unless there is a wait state or another bus request.
(But a HOLD will block the next bus request.)
The remaining gates end the cycle after T0 to preempt a prefetch if a CORR or SUSP micro-instruction occurs (d), or
end after T1 for a HALT (e).
The BUS-ACTIVE circuit above uses a complex gate, a 5-input NOR gate fed by 5 AND gates with two attached OR gates. Surprisingly,
this is implemented in the processor as a single gate with 14 inputs.
Due to how gates are implemented with NMOS transistors, it is straightforward to implement this as a single gate.
The inverter and NOR gate on the left, however, needed to be implemented separately, as they involve inversion;
an NMOS gate must have a single inversion.
The diagram above shows the layout of the bus state machine circuitry on the die, zooming in on the top region of the die. The metal layer has been removed to expose the underlying silicon and polysilicon. The layout of each flip-flop is completely different, since the layout of each transistor is optimized to its surroundings. (This is in contrast to later processors such as the 386, which used standard-cell layout.) Even though the state machine consists of just a handful of flip-flops and gates, it takes a noticeable area on the die due to the large 3.2 µm feature size of the 8088. (Modern processors have features measured in nanometers, not micrometers.)
Conclusions
The bus state machine is an example of how the 8088's design consists of complications on top of complications.
While the four-state bus cycle seems straightforward at first, it gets more complicated due to prefetching,
wait states, the HALT instruction, and the bus hold feature, not to mention the interactions between these features.
While there were good motivations behind these features, they made the processor considerably more complicated.
Looking at the internals of the 8088 gives me a better understanding of why simple RISC processors became popular.
The bus state machine is a key part of the read and write circuitry, moving the bus operation through the necessary T-states. However, the state machine is not the only component in this process; a higher-level circuit decides when to perform a read, write, or prefetch, as well as breaking a 16-bit operation into two 8-bit operations.11 These circuits work together with the higher-level circuit telling the state machine when to go through the states.
In my next blog post, I'll describe the higher-level memory circuit so follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon as oldbytes.space@kenshirriff. If you're interested in the 8086, I wrote about the 8086 die, its die shrink process, and the 8086 registers earlier.
Notes and references
-
The 8085 and 8088 processors both use a 4-step bus cycle for instruction fetching. For other reads and writes, the 8085's bus cycle has three steps compared to four for the 8088. Thus, the 8085 and 8088 bus cycles are similar but not an exact match. ↩
-
The 8088 has separate instructions to read or write an I/O device. From the bus perspective, there's no difference between an I/O operation and a memory operation except that a pin on the chip indicates if the operation is for memory or I/O.
The 8088 supports I/O operations for historical reasons, going back through the 8086, 8080, 8008, and the Datapoint 2200 system. In contrast, many other contemporary processors such as the 6502 used memory-mapped I/O, using standard memory accesses for I/O devices.
The 8086 has a pin M/IO that is high for a memory access and low for an I/O access. External hardware uses this pin to determine how to handle the request. Confusingly, the pin's function is inverted on the 8088, providing IO/M. One motivation behind the 8088's 8-bit bus was to allow reuse of peripherals from the earlier 8-bit 8085 processor. Thus, the pin's function was inverted so it matched the 8085. (The pin is only available when the 8086/8088 is used in "minimum mode"; "maximum mode" remaps some of the pins, making the system more complicated but providing more control.) ↩
-
I've made the timing diagram somewhat idealized so actions line up with the clock. In the real datasheet, all the signals are skewed by various amounts so the timing is more complicated. See the datasheet for pages of timing constraints on exactly when signals can change. ↩
-
For more information on the implementation of the address adder, see my previous blog post. ↩
-
The
POPoperation is an example of how the address adder updates a memory pointer. In this case, the stack address is moved from the Stack Pointer to theINDregister in order to perform the memory read. As part of the read operation, theINDregister is incremented by 2. The address is then moved from theINDregister to the Stack Pointer. Thus, the address adder not only performs the segment arithmetic, but also computes the new value for theSPregister.Note that the increment/decrement of the
INDregister happens after the memory operation. For stack operations, the SP must be decremented before aPUSHand incremented after aPOP. The adder cannot perform a predecrement, so thePUSHinstruction uses the ALU (Arithmetic/Logic Unit) to perform the decrement. ↩ -
During the
CORRmicro-instruction, the Bus Interface Unit performs specialTSandT0states. Note that these states don't have any external effect, so they are invisible outside the processor. ↩ -
The tradeoff with memory boards was that slower RAM chips were cheaper. The better RAM boards advertised "no wait states", but cheaper boards would add one or more wait states to every access, reducing performance. ↩
-
Only the second half of the
TSstate has an effect on the Bus Interface Unit, soTSis not a full state like the other states. Specifically, a delayedTSsignal is taken from the first half of theT0flip-flop, and this signal is used to control various actions in the Bus Interface Unit. (Alternatively, you could think of this as an earlyT0state.) This is why there isn't a separate flip-flop for theTSstate. I suspect this is due to timing issues; by the time theTSstate is generated by the logic, there isn't enough time to do anything with the state in that half clock cycle, due to propagation delays. ↩ -
There is a bit more circuitry for the
T1state for aHALT. Specifically, there is a flip-flop that is set on this signal. On the next cycle, this flip-flop both blocks the generation of anotherT1state and blocks the previousT1state from progressing toT2. In other words, this flip-flop makes sure the specialT1lasts for one cycle. However, aHOLDstate resets this flip-flop. That allows another specialT1to be generated when theHOLDends. ↩ -
The trickiest part of this circuit is using
T1-preto start a (short) cycle forHALT. The way it works is that theT1-presignal only makes a difference if there isn't a bus cycle already active. The only way to get an "unexpected"T1-presignal is if the state machine generates it for the first cycle of aHALT. Thus, theHALTtriggersT1-preand thus thebus-activesignal. You might wonder why thebus-activeuses this roundabout technique rather than getting triggered directly byHALT. The motivation is that the specialT1state forHALTrequires the AND of three signals to ensure that the state is generated once for theHALTrather than continuously, but happens again after aHOLD, and waits until the current bus cycle is done. Instead of duplicating that AND gate, the circuit usesT1-prewhich incorporates that logic. (This took me a long time to figure out.) ↩ -
The 8088 has a 16-bit bus, compared to the 8088's 8-bit bus. Thus, a 16-bit bus operation on the 8088 will always require two 8-bit operations, while the 8086 can usually perform this operation in a single step. However, a 16-bit bus operation on the 8086 will still need to be broken into two 8-bit operations if the address is unaligned (i.e. odd). ↩